rownanie prostej bedacej osia symetrii dwoch okregow iza: błagam Was o pomoc! nie kamam: wyznacz równanie prostej będącej osią symetrii dwóch okregów: (x−2)² + (y+2)²=1 i x² + y² +4x−1=0 Drugą postac zamienilam na postac kanoniczna i oba dalam do rownania wyszlo mi, ze y=−2 po narysowanbiu zobaczylam, ze os symetrii jest równa dla x=2 ale nic z tego nie rozumiem jak mam to zadanie rozwiązać i jaka jest odpowiedź,,,blagam o pomoc

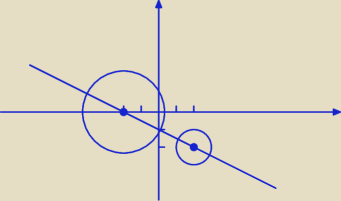Godzio: (x − 2)² + (y + 2)² = 1 (x + 2)² + y² = 5 Osią symetrii dwóch okręgów jest zawsze prosta przechodząca przez ich środki. S₁(2,−2) S₂(−2,0) Wyznacz teraz prostą przechodzącą przez dwa punkty

iza: czyli y=−2x−4? i to jest rozwiązanie?

Godzio:

	1
Nie, y = −		x − 1
	2

iza: tak przepraszam, źle obliczyłem współczynnik kierunkowy dziekuje

iza: i to jest ta prosta tak?

zia: pomylak mialo byc (x − 2) ² + y2 = 5