Zadanie Nika: W trójkąt równoramienny o kącie przy podstawie równym 3o stopni wpisano okrąg o promieniu 2. Oblicz pole tego trójkąta.

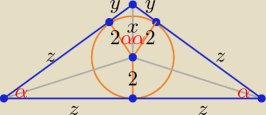
Bogdan: α = 30^o Korzystam z własności trójkąta prostokątnego o kącie ostrym 30^o.

	2		4
2 = y√3 ⇒ y =		√3, x = 2y =		√3
	3		3

	4
z = (2 + x)√3 = (2 +		√3)*√3 = 2√3 + 4
	3

Teraz pole trójkąta można już łatwo obliczyć.

takietosmutne: ale dziwnie ja nie rozumiem nic i tak

takietosmutne: liczyłam innym sposobem i nie rozumiem czemu mi nie wyszło.. zrobilam tak: r to 1/3 h , wiec h = 6 później z cos 60 stopni wyliczyłam a czyli 1/2=6/a , no bo tak wnioskuje, że skoro przy podstawie jest 30 stopni to u góry 120, 120:20, to daje nam 60 i a wyszło 12, moje "a" to wasze "y+z", a b wyszło mi 12 pierwiastków z 3, wiec pole wyszło 36 pierwiastków z 3 ............ proszę o pomoc, co zrobilam źle

Mila:

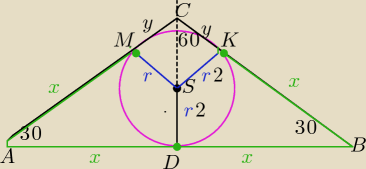
	1
To nie jest trójkąt równoboczny i nie możesz korzystać z zależność, że r=		h
	3

Na rysunku masz zaznaczone odcinki o jednakowych długościach: Punkty styczności okręgu są jednakowo odległe od wierzchołka kąta. Środek okręgu wpisanego w Δ leży na przecięciu dwusiecznych kątów Δ. w Δ CKS: (Δ o kątach 90,60,30)

	r
sin60=
	CS

	2
U{√3{2}}=
	CS

√3*|CS|=4 /*√3 3|CS|=4√3

	4√3
|CS|=
	3

	4√3
|CD|=h=2+
	3

W ΔCDB:

	h
tg30=
	x

√3		h
	=
3		x

	√3		4√3		√3
h=x*		⇔2+		=x*		/*3
	3		3		3

6+4√3=x*√3 /*√3 6√3+12=3x x=2√3+4 , |AB|=2x

	1
PΔ=		*2x*h
	2

	4√3
PΔ=x*h =(2√3+4)*(2+		) dokończ
	3

kaśka123: nie rozumiem

xd: Ω∞≤≥∊⊂α∫←→⇒⇔