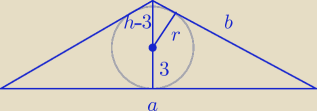
 Na okręgu o promieniu 3 opisano trójkąt równoramienny o kącie przy wierzchołku równym
120stopni. Oblicz długości boków tego trójkąta.
Na okręgu o promieniu 3 opisano trójkąt równoramienny o kącie przy wierzchołku równym
120stopni. Oblicz długości boków tego trójkąta.
| r | 2r | |||
sin60o = | ⇒ h = | + 3 = 2√3 + 3 | ||
| h − 3 | √3 |
| h | h | |||
sin30o = | ⇒ b = | = 4√3 + 6 | ||
| b | sin30o |
| ||||||||
ctg30o = | ⇒ a = 2√3(2√3 + 3) = 12 + 6√3 | |||||||
| h |
