PONAWIAM PROŚBE! Karolinka: Dana jest funkcja f(x)= tgx/|tgx| gdzie x ∈<-π,π> a) zapisz wzór tej funkcji bez użycia wartości bezwzględnej b)rozwiąż nierówność f(x)<0

Basia: rozwiązuję

Basia: (a) x∈<-π; 0) ⇒ tgx < 0 ⇒ |tgx| = -tgx x∈<0;π> ⇒ tgx ≥ 0 ⇒ |tgx| = tgx czyli: tgx / (-tgx) = -1 dla x∈(-π;0) f(x) = tgx / tgx = 1 dla x∈<0;π> -1 dla x∈(-π;0) f(x) = 1 dla x∈<0;π> (b) f(x) < 0 ⇔ f(x) = -1 ⇔ x∈(-π;0)

janek618: chyba Basia ma źle , bo powinno być : 1 dla tgx ≥ 0 i −1 dla tgx < 0

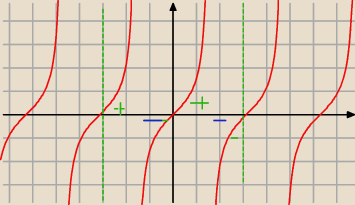
Aga1.: Oto wykres y=tgx

	π		π
f(x)=1 gdy tgx>0 , czyli dla x∊(−π,−		)U(0,		)
	2		2

f(x)=−1 gdy x∊(−π/2,0)U(π/2,π)