Funkcja liniowa Kwolas: Sprawdź, czy punkty A, B, C należą do wykresu tej samej funkcji liniowej. a) A(−4,1) B(8,7) C(−6,8) b) A(2, −7) B(3,−10) C(−2,5)

Kamila :

Kamila :

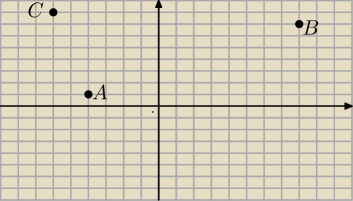
#k: Jest wiele sposobów na sprawdzenie tego czy punkty sa wspóliniowe Np taki podpunkt a) LIcze współczynnik kierunkowy (m) prostej przechodzącej przez punkty A i B

	yB−ya		7−1		6		1
m=		=		=		=
	xB−xA		8+4		12		2

	1
m=
	2

Piszse rownanie prostej przechodzącej przez punkty A i B Do obliczen biore punkt A (−4,1) czyli x₀=−4 y₀=1 y=m(x−x₀)+y₀

	1
y=		(x+4)+1
	2

	1
y=		x+3
	2

sprawdzam czy punkt C nalezy do prostej AB Wstawiam wspolrzedne punktu C do rownania prostej AB

	1
y=		x+3
	2

	1
8=		*(−6)+3
	2

8≠0 Punkty nie są wspoliniowe czyli nie należą do tej samej prostej co widac na rysunku tak samo zrób podpunkt b)

alex: Nie trzeba wyznaczać równań prostych, wystarczą współczynniki kierunkowe

	6		1		7
a) współczynniki kierunkowe prostych: aAB =		=		, aAC =
	12		2		−2

nie są współliniowe

	−3		12
b) aAB =		= −3, aAC =		= −3, są współliniowe
	1		−4

Mila: Można skorzystać z wektoróW a) AB^→=[12,6] AC^→=[−2,7] Czy istnieje k∊R t.że: [12,6]=k*[−2,7] ? −2k=12 i 7k=6 ?

	6		6
k=−6 i k=		−6≠
	7		7

........, punkty nie są współliniowe b) AB^→=[1,−3] AC^→[−4, 12] [1,−3]=k*[−4, 12]

	−1
−4k=1⇔k=
	4

	−1
12k=−3⇔ k=		punkty są współliniowe
	4