geometria Biały: Proszę o pomoc Dwie wysokości trójkąta ABC, gdzie A=(−2,−3), zawarte są w prostych o równaniach x−2=0 i 2x+3y−1=0. Oblicz współrzędne pozostałych wierzchołków tego trójkąta. Kombinuję, kombinuję i nic nie wychodzi. Jakbym miał przynajmniej dwa wierzchołki to skorzystałbym ze wzoru na środek ciężkości, bo go łatwo obliczyć

Biały: to jak, znajdzie się jakiś chętny do pomocy?

Biały: Idę spać, mam nadzieję, że jak rano wstanę to jakaś dobra osoba już mi powie jak to zrobić

Gustlik: Musisz sobie to dokładnie rozrysować: Twoje proste − wysokości to po przekształceniu do bardziej czytelnych postaci mają równania: prosta h_C: x=2

	2
prosta hB: y=−		x+U{1]{3}
	3

Prowadzę z punktu A prosta prostopadłą do h_B − będzie to prosta zawierająca bok AC:

	3		3
y=		x+b, po podstawieniu współrzędnych A b=0,zatem prosta AC ma równanie y=		x,
	2		2

prosta ta przecina się z prostą x=2 tworzac wierzchołek C: Rozwiązuje układ równań i otrzymuję współrzędne C:

	3
{ y=		x
	2

{ x=2 Zatem C=(2, 3) Prowadzę teraz prostą AB prostopadłą do x=2 aż do punktu przecięcia z prostą h_B:

	2
y=−		x+U{1]{3}
	3

Prosta AB jako prostopadła do prostej pionowej x=2 jest pozioma i ma równanie y=−3 (jak współrzędna y punktu A). Rozwiązuję układ równań:

	2
{ y=−		x+U{1]{3}
	3

{ y=−3

	2
−3=−		x+U{1]{3} /*3
	3

−9=−2x+1 −10=−2x /:(−2) x=5 Zatem B=(5, −3).

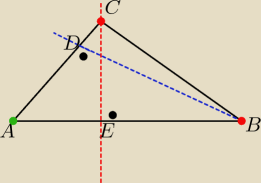
Eta: Punkt A nie należy do zadnej z tych wysokości ( pomyśl , dlaczego? zatem wysokości są poprowadzone z wierzchołków B i C prosta zawierająca wysokość BD: x−2=0 jest prostopadła do boku AC to równanie prostej zawierającej bok AC: y= y_A => AC: y= −3 zatem punkt C( x, −3) prosta zawierająca wysokość CE: 2x +3y −1=0 i C( x, −3) to: 2x −9−1=0 => x= 5 to; C( 5, −3)

	2		1		2
CE: y= −		x +		......... wsp. kier. a1= −
	3		3		3

to prosta AB jest prostopadła do CE i zawiera punkt A ma równanie:

	3		3
AB: y=		(x−xA) +yA) => AB: y=		x:
	2		2

Punkt B nalezy do wysokości BD : x−2=0 => B( 2,y)

	3
i B należy również do prostej AB : y=		x
	2

	3
to: y=		*2= 3 zatem B(2, 3)
	2

Miłych snów, zadanie rozwiązane

Biały: Załóżmy dotarłbym do jednego z punktów( mam dwa ale nie mam trzeciego). To nie mógłbym wyznaczyć pkt. D będący środkiem ciężkości trójkąta ABC i później podstawić w ten sposób

xA + xB + xC		yA + yB + yC
	=współrzędna x z pkt. D oraz		=współrzędna x z pkt. D
3		3

No i jest mały mankament, bo wynik, który mi wychodzi to pkt. mający współrzędne (6,−3)