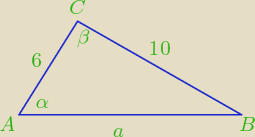
planimetria olkaaa: W trójkącie ostrokątnym ABC danymi są: |AC|=6 , |BC|=10 , jego pole= 15√3. Oblicz długość |AB|, sin ∡BAC, pole koła opisanego na tym trójkącie i długość r okręgu wpisanego w trójkąt. Jest tutaj do wykorzystania sporo wzorów. Nie proszę o rozwiązanie, a co po kolei zrobić. Chyba trzeba zacząć od rozpisania pola na jakiś szalony wzór. Pomoże ktoś?

Godzio:

	1		√3
P =		* 6 * 10 * sinβ ⇒ sinβ =		⇒ β = 60o
	2		2

Z tw. cosinusów wyznaczyć długość boku "a" Z tw. sinusów wyznaczyć sinus kąta α i promień okręgu opisanego Mając promień okręgu opisanego obliczysz pole koła

	2P
Długość promienia okręgu wpisanego obliczysz ze wzoru: r =		− wszystko masz
	a + b + c

dane

olkaaa: ooooo , głupia ja

olkaaa: uwagę mam, bok a powinien być na przeciwko kąta alfa, natomiast sinus kąta możemy już walnąć z kąta przy wierzchołku C, bo z cosinusów walnęliśmy bok naprzeciw, co nie?

Godzio: A dlaczego α ma być na przeciwko a ? To robi jakąś różnicę ?