Trygonometria
;): | 1 | | 1 | | π | |
| + |
| = √8 sinx ≠ kπ k∊C ⋀ cosx ≠ |
| + kπ k∊C |
| sinx | | cosx | | 2 | |
√8sinxcosx = sinx + cosx /
2
8(sinxcosx)
2 = 1 + 2sinxcosx
8(sinxcosx)
2 − 2sinxcosx − 1 = 0
sinxcosx = t
8t
2 − 2t − 1 = 0
Δ = 1 + 8
√Δ = 3
| | 1 − 3 | | 1 | | 1 | |
t1 = |
| = − |
| sinxcosx = − |
| |
| | 8 | | 4 | | 4 | |
| | 1 + 3 | | 1 | | 1 | |
t2 = |
| = |
| sinxcosx = |
| |
| | 8 | | 2 | | 2 | |
Teraz pytanko jak to dalej rozwiązać? Dziękuję z góry za odpowiedź

25 maj 23:03
Godzio:
Taki szczegół:
| | π | |
x ≠ kπ i x ≠ |
| + kπ k∊C |
| | 2 | |
25 maj 23:05
;): Na górze napisałem dziedzinkę
Godzio
Oczywiście zawsze na Ciebie można liczyć i zawsze wszystko widzisz dziękuję Ci bardzo

25 maj 23:07
Godzio:
Można to też tak zrobić:
√8sinxcosx = sinx + cosx /:
√2
| | √2 | | √2 | |
2sinxcosx = |
| sinx + |
| cosx |
| | 2 | | 2 | |
| | π | | π | |
2x = x + |
| + 2kπ lub 2x = π − x − |
| + 2kπ |
| | 4 | | 4 | |
x = ... lub x = ...
25 maj 23:08
Godzio:
No tak, tylko że ty napisałeś sinx ≠ kπ, a nie x

25 maj 23:08
;): Rzeczywiście chciałem napisać sinx ≠ 0 a napisałem od razu wynik zamiast 0

Takie ciekawe
zadanka znalazłem może chcesz kilka?

25 maj 23:11
Godzio:
Jak jakieś trudniejsze możesz dać

25 maj 23:11
Godzio:
Tak się zastanawiam czy po przez podniesienie do kwadratu nie dokładasz rozwiązań hmmm ?
25 maj 23:12
;): Można sprawdzić czy podnosząc do kwadratu wychodzą te same wyniki to u Ciebie

25 maj 23:13
;): A tylko powiedz jaki dział czy obojętne co Ci dać?

25 maj 23:14
Godzio:
Ale raczej nie powinno się tak robić, weźmy prosty przykład:
x − 1 = 2x + 1
x = − 2
x − 1 = 2x + 1 /2
x2 − 2x + 1 = 4x2 + 4x + 1
3x2 + 6x = 0
3x(x + 2) = 0
x = 0 lub x = − 2
I nie wychodzi dokładnie to samo, u Ciebie wyjdą 3 rozwiązania u mnie dwa
25 maj 23:15
Godzio: Obojętnie

25 maj 23:15
;): Na przyszłość zapamiętam jeszcze raz wielkie dzięki
 Posługując się rachunkiem różniczkowym określić liczbę rozwiązań równania
Posługując się rachunkiem różniczkowym określić liczbę rozwiązań równania
2x
3 + 1 = 6|x| − 6x
2
25 maj 23:18
;): Takie na rozgrzewkę Ci dałem

25 maj 23:21
Godzio:
Skąd bierzesz te zadania, bo chyba się domyślam ?
To zadanie robiłem już, była taka sama treść, tyle że rachunkiem różniczkowym tego nie zrobię

25 maj 23:22
;): Znalazłem przez przypadek na stronie jednej jakieś Prace Kontrolne czy coś takiego

25 maj 23:25
Godzio:
Tak myślałem

Korespondencyjny kurs z matematyki
http://www.im.pwr.wroc.pl/kurs/
Tego zadania niestety nie zrobię, bo trzeba mieć nieco większą wiedzę
25 maj 23:29
;): Właśnie dokładnie z tej stronki będę miał co w między czasie robić

To książka do reki i jutro
widzę zadanie zrobione oczywiście żartuje

25 maj 23:32
Godzio:

Mam zbiór zadań 1999−2004 z odpowiedziami i wskazówkami, także jakbyś chciał sprawdzić to służę
pomocą

25 maj 23:33
;): Oo naprawdę to jak coś to niestety ale będę musiał Cię ponękać troszkę

25 maj 23:36
;): Ale jak tak patrzę na te Prace Kontrolne to z roku na rok chyba łatwiejsze robią

25 maj 23:37
Godzio:
Ano, kiedyś poziom był wyższy

Osobiście wysyłałem w tym roku zadania, i też znowu aż takie wszystko oczywiste nie było
25 maj 23:38
;): | 8 | | 9 | |
| (sin2x + sin4x + ... ) = 4 − 2cosx + 3cos2x − |
| cos3x + ... |
| 3 | | 2 | |
q
1 = sin
2x
S
n1 = tg
2x
| | −2cosx | |
Sn2 = |
| → można coś z tym dalej zrobić czy nie bardzo? |
| | | |
25 maj 23:45
Godzio:
Żeby można było skorzystać ze wzoru na sumę to
|q| < 1 ⇒ x ∊ ...
Jedynie tyle:
25 maj 23:52
Godzio:
| | 1 − cos2x | |
Żeby to rozwiązać, proponowałbym jednak S1 = |
| |
| | cos2x | |
i cosx = t
Tak chyba najłatwiej by było
25 maj 23:59
;): | 8 | | 8 + 8cosx | | 1 | |
| tg2x = |
| / * |
| |
| 3 | | 2 + 3cosx | | 8 | |
| 1 | | 1 + cosx | |
| tg2x − |
| |
| 3 | | 2 + 3cosx | |
| 2 + 3cosx − cosx − cos2x | |
| = 0 |
| 2cosx + 3cos2x | |
| −cos2x + 2cosx + 2 | |
| = 0 |
| 2cosx + 3cos2x | |
cosx = t
−t
2 + 2t + 2 = 0
Δ = 1 + 2
√Δ =
√3
t
1 = 2 +
√3
t
2 = 2 −
√3
Hmm dobrze jest to
Godzio 
?
26 maj 00:06
;): Ech nie zauważyłem Twojego wpisu wyżej bo robiłem to zadanie
26 maj 00:07
;): Oczywiście t∊<−1,1> więc t1 odpada i zostaje t2 = 2 − √3
26 maj 00:11
Godzio:
| 8 | | 1 − t2 | | 4t | |
| * |
| = 4 − |
| |
| 3 | | t2 | | 2 + 3t | |
| 2 | | 1 − t2 | | t | |
| * |
| = 1 − |
| |
| 3 | | t2 | | 2 + 3t | |
| 1 − t2 | | t + 1 | |
| = |
| |
| 3t2 | | 2 + 3t | |
(1 − t
2)(2 + 3t) = 3t
2(t + 1)
3t
2(t + 1) + (t
2 − 1)(2 + 3t) = 0
(t + 1)(3t
2 + 2t + 3t
2 − 2 − 3t) = 0
(t + 1)(6t
2 − t − 2) = 0
(t + 1)(2t + 1)(3t − 2) = 0
| | 1 | | 2 | |
t = − 1 − to wypadnie za pewne ze względu na D, lub t = − |
| lub t = |
| − odpada |
| | 2 | | 3 | |
| | 2 | | 2 | |
x = |
| π + 2kπ lub x = − |
| π + 2kπ |
| | 3 | | 3 | |
26 maj 00:58
;): Jak coś to jutro zobaczę kolejne zadanie i dziękuję za pomoc

Dobranoc

26 maj 01:58
Godzio:
Dobranoc

26 maj 02:00
;): Kolejne zadanko to sprawdzenia

3
x + 1 + 3
−x + ... = 4
| | 1 | |
|q| < 1 ⇒ ( |
| )x < 1 x > 0 |
| | 3 | |
| 32x | |
| = 4 / * (3x − 1) |
| 3x − 1 | |
3
2x = 4 * 3
x − 4
3
2x − 4 * 3
x + 4 = 0
(3
x − 2)
2 = 0
3
x = 2
x = log
32
26 maj 14:41
;): Rozwiąż równanie
cos4x = sin3x
cos4x − sin3x = 0
| | π | | π | | π | |
sin3x = cos( |
| − 3x) = cos(−(3x − |
| )) = cos(3x − |
| ) |
| | 2 | | 2 | | 2 | |
| | π | |
cos4x − cos(3x − |
| ) = 0 |
| | 2 | |
Teraz nie wiem czy mogę skorzystać z wzoru cosα − cosβ ?
Czyli
| | | |
| = kπ / * 2 ⋁ |
| = kπ / * 2 |
| 2 | | 2 | |
| | π | | 1 | | π | |
7x = |
| + 2kπ / * |
| ⋁ x = − |
| + 2kπ |
| | 2 | | 7 | | 2 | |
| | π | | 2 | | π | |
x = |
| + |
| kπ k∊C ⋁ x = − |
| + 2kπ k∊C |
| | 14 | | 7 | | 2 | |
Czy w ogóle jest to dobrze?
26 maj 15:43
Bogdan:
| | π | |
cos4x = sin3x ⇒ cos4x = cos( |
| − 3x) |
| | 2 | |
| | π | | π | |
4x = |
| − 3x + k*2π lub 4x = − |
| + 3x + k*2π |
| | 2 | | 2 | |
| | π | | π | |
7x = |
| + k*2π lub x = − |
| + k*2π |
| | 2 | | 2 | |
| | π | | 2π | | π | |
x = |
| + k* |
| lub x = − |
| + k*2π |
| | 14 | | 7 | | 2 | |
26 maj 15:49
;): Jeju a ja rozpisywałem to na wzory Dziękuję bardzo
Bogdanie będę musiał nauczyć się na
szybko robić bez zbędnych liczeń

26 maj 15:52
;): A mógłbyś
Bogdanie jeszcze zerknąć na to powyżej zadanie?

26 maj 15:54
Bogdan:
zadanie z szeregiem geometrycznym jest dobrze rozwiązane
26 maj 15:57
;):
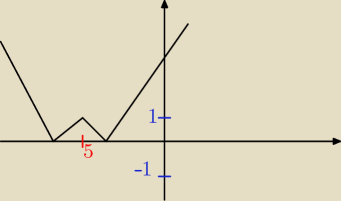
Dziękuję bardzo

Teraz ostatnie jak coś może później jeszcze porobię
Zbadaj liczbę równania w zależności od parametru m
||x + 5| − 1| = m
y = x
→| | y = |x|
→Tu→ = [−5,0] y = |x + 5|
→{Tu
→ = [0,−1]}
y = |x + 5| − 1 →
| | y = ||x + 5| − 1|
m∊(−
∞,0) → 0 rozw.
m = 0 → 2 rozw.
m∊(0,1) → 4 rozw.
m = 1 → 3 rozw.
m∊(1,
∞) → 2 rozw.
26 maj 16:09


 Oczywiście zawsze na Ciebie można liczyć i zawsze wszystko widzisz dziękuję Ci bardzo
Oczywiście zawsze na Ciebie można liczyć i zawsze wszystko widzisz dziękuję Ci bardzo

 Takie ciekawe
zadanka znalazłem może chcesz kilka?
Takie ciekawe
zadanka znalazłem może chcesz kilka? 




 Posługując się rachunkiem różniczkowym określić liczbę rozwiązań równania
2x3 + 1 = 6|x| − 6x2
Posługując się rachunkiem różniczkowym określić liczbę rozwiązań równania
2x3 + 1 = 6|x| − 6x2



 Korespondencyjny kurs z matematyki
http://www.im.pwr.wroc.pl/kurs/
Tego zadania niestety nie zrobię, bo trzeba mieć nieco większą wiedzę
Korespondencyjny kurs z matematyki
http://www.im.pwr.wroc.pl/kurs/
Tego zadania niestety nie zrobię, bo trzeba mieć nieco większą wiedzę
 To książka do reki i jutro
widzę zadanie zrobione oczywiście żartuje
To książka do reki i jutro
widzę zadanie zrobione oczywiście żartuje
 Mam zbiór zadań 1999−2004 z odpowiedziami i wskazówkami, także jakbyś chciał sprawdzić to służę
pomocą
Mam zbiór zadań 1999−2004 z odpowiedziami i wskazówkami, także jakbyś chciał sprawdzić to służę
pomocą 


 Osobiście wysyłałem w tym roku zadania, i też znowu aż takie wszystko oczywiste nie było
Osobiście wysyłałem w tym roku zadania, i też znowu aż takie wszystko oczywiste nie było
 ?
?
 Dobranoc
Dobranoc

 3x + 1 + 3−x + ... = 4
3x + 1 + 3−x + ... = 4


 Dziękuję bardzo
Dziękuję bardzo Teraz ostatnie jak coś może później jeszcze porobię
Zbadaj liczbę równania w zależności od parametru m
||x + 5| − 1| = m
y = x →| | y = |x| →Tu→ = [−5,0] y = |x + 5| →{Tu→ = [0,−1]}
y = |x + 5| − 1 →| | y = ||x + 5| − 1|
m∊(−∞,0) → 0 rozw.
m = 0 → 2 rozw.
m∊(0,1) → 4 rozw.
m = 1 → 3 rozw.
m∊(1,∞) → 2 rozw.
Teraz ostatnie jak coś może później jeszcze porobię
Zbadaj liczbę równania w zależności od parametru m
||x + 5| − 1| = m
y = x →| | y = |x| →Tu→ = [−5,0] y = |x + 5| →{Tu→ = [0,−1]}
y = |x + 5| − 1 →| | y = ||x + 5| − 1|
m∊(−∞,0) → 0 rozw.
m = 0 → 2 rozw.
m∊(0,1) → 4 rozw.
m = 1 → 3 rozw.
m∊(1,∞) → 2 rozw.