ge mis: 4. Krótsza przekątna równoległoboku jest równa 3cm i tworzy z jednym z boków kąt 30 stopni. Kąt ostry równoległoboku jest równy 60 stopni. Oblicz pole i obwód tego równoległoboku.

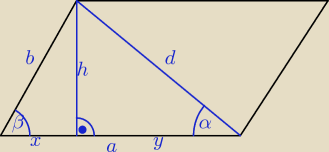
Anna: Dane: d=3cm, α=30⁰, β= 60⁰ P, ob = ? P=ah, ob=2a+2b

h
	= sinα
d

h
	= sin300 ⇒ h=1,5
3

h
	= sinβ
b

1,5
	= sin600
b

1,5		√3
	=		⇒ b=√3
b		2

	h
		= tgβ
	x

	1,5		1,5		√3
		= √3 ⇒ x=		=
	x		√3		2

	h
		= tgα
	y

	1,5		1,5		√3		4,5		3√3
		= tg300 ⇒		=		⇒ y=		=
	y		y		3		√3		2

	√3		3√3
a= x+y=		+		= 2√3
	2		2

P= 2√3*1,5 = 3√3cm² ob= 2*2√3 + 2*√3 = 6√3cm

Eta: 2 sposób ΔABD i ΔBCD są prostokątne o kątach : 30^o, 60^o, 90^o

	b*3
P= 2P(ΔABD)=2*		= 3b , Ob= 2a+2b
	2

b		b		√3
	= tg30o =>		=		=> b= √3
3		3		3

3		3		√3
	= sin60o =>		=		=> a= 2√3
a		a		2

P= 3b = 3√3 cm² Ob= 2a+2b= 4√3+2√3= 6√3 cm