geometria analityczna Tak, myślę, że tak: Zadania z geometrii analitycznej. Ważne 1] Przekątna kwadratu opisanego na okręgu o równaniu x²+y²−2x−4=0 zawiera się w prostej o równaniu 2x−y−2=0. Wyznacz współrzędne wierzchołków tego kwadratu. 2] Podstawa AB trójkąta równoramiennego ABC zawarta w prostej x+y+1=0. Ramię BC zawiera się w prostej 2x−y−1=0. Wyznacz równanie prostej k zawierającej ramię AC wiedząc, że pkt. P=(−4,0) należy do prostej k. Z góry dziękuję za pomoc. Mam więcej takich zadań i dobrze by było, żebym miał jakiś wzór to może bym coś zrozumiał

Tak, myślę, że tak: To jak, pomoże mi ktoś?

Godzio: Trochę roboty jest, ale zaraz pomogę ...

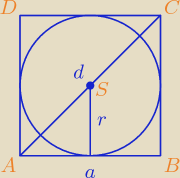
Godzio: x² + y² − 2x − 4 = 0 ⇒ (x − 1)² + y² = 5 ⇒ S(1,0), r = √5 a = 2r = 2√5 d = a√2 = 2√10 |AS| = √10 /² (1 − x)² + y² = 10 , y = 2x − 2 1 − 2x + x² + 4x² − 8x + 4 = 10 5x² − 10x − 5 = 0 x² − 2x − 1 = 0 Δ = 4 + 4 = 8

	2 + 2√2
x1 =		= 1 + √2 ⇒ y1 = 2 + 2√2 − 2 = 2√2
	2

x₂ = 1 − √2 ⇒ y₂ = 2 − 2√2 − 2 = − 2√2 A(1 − √2, −2√2) C(1 + √2, 2√2) Prosta prostopadła przechodząca przez S:

	1
a = −		S(1,0)
	2

	1		1
0 = −		+ b ⇒ b =
	2		2

	1		1
y = −		x +		⇒ 2y = −x + 1 ⇒ x = 1 − 2y
	2		2

|BS| = √10 /² (1 − x)² + y² = 10 x = 1 − 2y (1 − 1 + 2y)² + y² = 10 5y² = 10 y² = 2 y = √2 ⇒ x = 1 − 2√2 lub y = −√2 ⇒ x = 1 + 2√2 B(1 + 2√2, √2) D(1 − 2√2, √2) Nanieś te współrzędne na układ współrzędnych, narysuj prostą i sprawdź czy nie pomyliłem się z wierzchołkami A z C lub B z D

Tak, myślę, że tak: B(1 + 2√2, √2) to nie powinno być B(1 + 2√2, −√2) ?

Tak, myślę, że tak: a ktoś wie jak te drugie zrobić? głupie pytanie, może lepiej czy ktos pomoże?

Godzio: Dlatego sprawdź bo nie byłem pewien, zaraz Ci napisz to 2, tylko trochę kosmiczne rachunki mi wychodzą więc chwilkę to zajmie

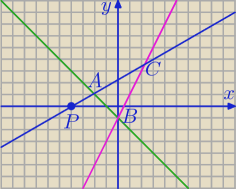
Godzio: Zad. 2 AB: y = − x − 1 BC: y = 2x − 1 AC: y = ax + b P(−4,0) ⇒ 0 = −4a + b ⇒ b = 4a ⇒ y = ax + 4a A:

	4a + 1
ax + 4a = − x − 1 ⇒ ax + x = − 4a − 1 ⇒ x = −
	a + 1

	4a + 1		3a
y = −x − 1 =		− 1 =
	a + 1		a + 1

	4a + 1		3a
A(−		,		)
	a + 1		a + 1

B(0,−1) C:

	4a + 1
2x − 1 = ax + 4a ⇒ 2x − ax = 4a + 1 ⇒ x =
	2 − a

	8a + 2		9a
y = 2x − 1 =		− 1 =
	2 − a		2 − a

	4a + 1		9a
C(		,		)
	2 − a		2 − a

Za chwilę dalsza część

Tak, myślę, że tak: Ok, dzięki za poświęcenie czasu. Nie lubię geometrii analitycznej, ale to pewnie dlatego, że jej nie rozumiem

Godzio: |AC| = |BC| (x_c − x_a)² + (y_c − y_a)² = x_c² + (y_c + 1)² x_c² − 2x_cx_a + x_a² + y_c² − 2y_cy_a + y_a² = x_c² + y_c² + 2y_c + 1 − 2x_cx_a + x_a² − 2y_cy_a + y_a² = 2y_c + 1 x_a² + y_a² = 2x_cx_a + 2y_cy_a + 2y_c + 1 I teraz kawałkami:

	16a2 + 8a + 1 + 9a2		25a2 + 8a + 1
xa2 + ya2 =		=
	(a + 1)2		(a + 1)2

	86a2 + 16a + 2
2xcxa + 2ycya =
	(2 − a)(a + 1)

25a2 + 8a + 1		86a2 + 16a + 2
	−		=
(a + 1)2		(2 − a)(a + 1)

	(25a2 + 8a + 1)(2 − a) − (86a2 + 16a + 2)(a + 1)
=		=
	(2 − a)(a + 1)2

	111a3 + 60a2 + 3a
= −
	(2 − a)(a + 1)2

I wracamy do równania:

	111a3 + 60a2 + 3a		18a
−		=		+ 1 /(2 − a)(a + 1)2
	(2 − a)(a + 1)2		2 − a

−111a³ − 60a² − 3a = 18a(a² + 2a + 1) + (2 − a)(a² + 2a + 1) 128a³ + 96a² + 24a + 2 = 0 /:2 64a³ + 48a² + 12a + 1 = 0 −− zauważamy wzór skróconego mnożenia

	1
(4a + 1)3 = 0 ⇒ a = −
	4

Równanie prostej k:

	1
y = −		x − 1
	4

Uffffffff mam nadzieję, że błędu nie popełniłem, pomijałem pewne przejścia, które polegały tylko na uproszczeniu wyrażeń

Godzio: W sumie bezmyślnie wysłałem ... prosta k ma dodatni współczynnik więc musiałem się gdzieś walnąć Narazie sobie to odpuszczę Jak wpadnę na jakiś prostszy pomysł to dam znać

Godzio: y = − x − 1 y = 2x − 1 Mamy taki wzorek:

	a1 − a2		−1 − 2
tgφ = |		| = |		| = 3
	1 + a1a2		1 − 2

Kąt między prostymi AB i AC musi być taki sam więc:

	a1 − a3		−1 − a3
tgφ = |		| = |		| = 3
	1 + a1a3		1 − a3

−1 − a3		−1 − a3
	= 3 lub		= − 3
1 − a3		1 − a3

−1 − a₃ = 3 − 3a₃ lub −1 − a₃ = −3 + 3a₃ 2a₃ = 4 lub 4a₃ = 2

	1
a3 = 2 lub a3 =
	2

	1
y = 2x + 8 lub y =		x + 2
	2

Pierwsza prosta jest równoległa do BC więc ją odrzucamy:

	1
Odp: y =		x + 2
	2

Heh, wystarczy chwilkę pomyśleć

dorotka: 1. przekątna kwadratu opisanego na okręgu o równaniu (x−1)² + y² = 5 jest zawarta w prostej 2x − y − 2 = 0. wyznacz współrzędne wierzchołków tego kwadratu. 2. Oblicz długość cięciwy, którą okrąg (x+3)² + (y−2)² = 16 wyznacza na prostej y = −x + 3