Stereometria
Godzio: Trudne zadanie dla chętnych 
Podstawą czworościanu ABCD jest trójkąt prostokątny ABC o kącie ostrym α i promieniu okręgu
wpisanego r. Spodek wysokości opuszczony z wierzchołka D leży w punkcie przecięcia się
dwusiecznych trójkąta ABC, a ściany boczne wychodzące z wierzchołka kąta prostego podstawy
tworzą kąt β. Obliczyć objętość tego ostrosłupa
24 maj 22:00
TOmek:
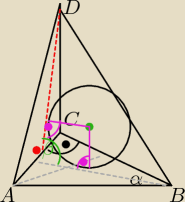
α<90
ciekawi mnie jak ma wyglądac te koło wpisane, dotyka one wysokosci scian bocznych, tak?
24 maj 22:24
Kejt: a to nie chodzi o koło wpisane w podstawę?
24 maj 22:25
TOmek: chyba masz racje
24 maj 22:54
Kejt:
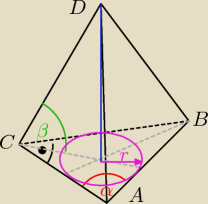
ja to widzę tak..
24 maj 23:02
TOmek: "a ściany boczne wychodzące z wierzchołka kąta prostego podstawy tworzą kąt β."
Moim zdaniem masz źle zaznaczony kąt β
24 maj 23:08
Kejt: to gdzie wg Ciebie będzie kąt β?
24 maj 23:10
TOmek:
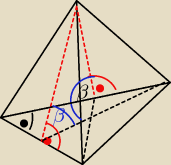
24 maj 23:15
Kejt: hmm.. to musimy chyba poczekać na eksperta..
24 maj 23:16
TOmek: dziwnie jest to sformułowane, ja odbieram to tak jak powyżej

24 maj 23:17
Kejt: ale to jutro.. ja znikam. dobranoc

24 maj 23:17
TOmek: Na mooje gdyby była krawedz do podstawy, to musiało być to twardo zapisane, dobra ja lece spac,
jutro tu wpadne, zobacze jak sie temat rozwinął

Dobranoc!
24 maj 23:18
Godzio:
Zaraz zrobię rysunek żeby nie było wątpliwości

24 maj 23:22
Godzio:
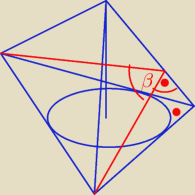
To jest po prostu kąt między dwiema ścianami bocznymi

24 maj 23:26
Godzio:
Podbijam

25 maj 15:35
TOmek: nigdy bym nie wpadł ,ze ten kąt ma tak wyglądac
25 maj 15:38
Godzio:
Zwykły kąt dwuścienny

25 maj 16:04
TOmek:
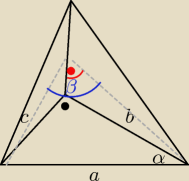
sinα*a=c
Niech chociaz ktoś powie ,czy jest na razie dobrze , bo nie wiem czy dalej robić

25 maj 16:17
Godzio:
Błędu chyba nie ma

25 maj 16:28
TOmek:
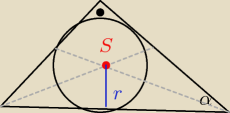
pózniej wyznacze w podobny sposob "b" i mam pole a*b/2
2
o. Teraz wysokosc
*dwusieczne są srodkiem okregu wpisanego, hmmm i co dalej ....
spadam na trening

25 maj 16:30
TOmek:
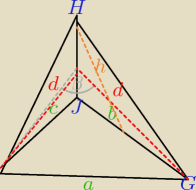
już wiem co dalej, musze obliczyć "d" np: tw. cosinusów.
i będę miec wysokość trójkąta GHJ, pózniej przyrównuje pola i będę miał "h" i mogę spokojnie
obliczyć "h" z r
2+H
2=d
2
taki mam pomysł, jak będę miał czas sprobujue to przelac na papier

25 maj 16:33
Godzio:
Podam odp:
| | √2 | | 1 + sinα | | β | | α | |
V = |
| r3 * |
| cos |
| ctg |
| |
| | 3 | | cosα√−cosβ | | 2 | | 2 | |
25 maj 16:59
Godzio:
I jak próbuje ktoś

?
25 maj 22:29
kv45: Pole podstawy można np tak:
| | 2P | |
r= |
| gdzie a=btgα oraz c=bsecα |
| | a+b+c | |
btgα=rtgα+r+rsecα
b=r+rctgα+rcscα
a zatem:
| | 1 | | 1 | | α | | α | |
P= |
| b2tgα = |
| r2(1+ctg |
| +ctg2 |
| )*tgα |
| | 2 | | 2 | | 2 | | 2 | |
ale co z wysokością

?
25 maj 23:28
kv45: tam powinno być "2" przed ctg{α}{2}
25 maj 23:30
ICSP: Godziu spójrz na wynik, nie dziwie się że nikomu się nie chciało

17 cze 16:24
Godzio:
No właśnie to ma zachęcić bo to jest świetne zadanie

17 cze 16:24
Godzio:
Dojść do takiego wyniku to jest mega satysfakcja

17 cze 16:25
ICSP: tylko że np. ja nie potrafię robić tego typu zadań. Sprawiają mi one olbrzymią trudność. No i
oczywiście nie potrafię wyznaczać funkcji np. połowy kąta:(
17 cze 16:27
Godzio:
E tam, odpowiedź można przedstawić w różnych postaciach, a dalej bawić się w dojście do tej z
podręcznika

17 cze 16:28
 Podstawą czworościanu ABCD jest trójkąt prostokątny ABC o kącie ostrym α i promieniu okręgu
wpisanego r. Spodek wysokości opuszczony z wierzchołka D leży w punkcie przecięcia się
dwusiecznych trójkąta ABC, a ściany boczne wychodzące z wierzchołka kąta prostego podstawy
tworzą kąt β. Obliczyć objętość tego ostrosłupa
Podstawą czworościanu ABCD jest trójkąt prostokątny ABC o kącie ostrym α i promieniu okręgu
wpisanego r. Spodek wysokości opuszczony z wierzchołka D leży w punkcie przecięcia się
dwusiecznych trójkąta ABC, a ściany boczne wychodzące z wierzchołka kąta prostego podstawy
tworzą kąt β. Obliczyć objętość tego ostrosłupa
 α<90
α<90
 ja to widzę tak..
ja to widzę tak..



 Dobranoc!
Dobranoc!

 To jest po prostu kąt między dwiema ścianami bocznymi
To jest po prostu kąt między dwiema ścianami bocznymi 





 pózniej wyznacze w podobny sposob "b" i mam pole a*b/2
2o. Teraz wysokosc
*dwusieczne są srodkiem okregu wpisanego, hmmm i co dalej ....
spadam na trening
pózniej wyznacze w podobny sposob "b" i mam pole a*b/2
2o. Teraz wysokosc
*dwusieczne są srodkiem okregu wpisanego, hmmm i co dalej ....
spadam na trening 
 już wiem co dalej, musze obliczyć "d" np: tw. cosinusów.
i będę miec wysokość trójkąta GHJ, pózniej przyrównuje pola i będę miał "h" i mogę spokojnie
obliczyć "h" z r2+H2=d2
taki mam pomysł, jak będę miał czas sprobujue to przelac na papier
już wiem co dalej, musze obliczyć "d" np: tw. cosinusów.
i będę miec wysokość trójkąta GHJ, pózniej przyrównuje pola i będę miał "h" i mogę spokojnie
obliczyć "h" z r2+H2=d2
taki mam pomysł, jak będę miał czas sprobujue to przelac na papier 

 ?
?
 ?
?



