planimetria olkaaa: W równoległoboku przekątna ma długość 7. Wiedząc, że obwód równoległoboku jest równy 26 i kąt ∡ABC ma 120^o oblicz długość boków równoległoboku.

olkaaa: nikt?

Godzio: Jest napisane która przekątna ?

olkaaa: nie ma, tutaj znalazłam jakieś dziwne zapiski: http://www.matematyka.pl/79468.htm może umiecie wyjaśnić to łopatologicznie?

Godzio: Nie dodałaś "przekątna DB "

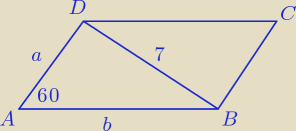
Godzio: 2a + 2b = 26 a + b = 13 a = 13 − b Z twierdzenia cosinusów: a² + b² − 2abcos(60^o) = 7²

	1
(13 − b)2 + b2 − 2 * (13 − b) * b *		= 49
	2

169 − 26b + b² + b² − 13b + b² = 49 3b² − 39b + 120 = 0 b² − 13b + 40 = 0 Δ = 169 − 160 = 9 √Δ = 3

	13 + 3
b1 =		= 8 ⇒ a = 5
	2

	13 − 3
b2 =		= 5 ⇒ a = 8
	2

olkaaa: świetnie, dzięki!