n vercia09028: 3^12x − 11* 3^8x + 19* 3^4x − 9≥0

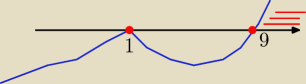
Godzio: 3^4x = t t > 0 t³ − 11t² + 19t − 9 ≥ 0 t³ − t² − 10t² + 10t + 9t − 9 ≥ 0 t²(t − 1) − 10t(t − 1) + 9(t − 1) ≥ 0 (t − 1)(t² − 10t + 9) ≥ 0 (t − 1)(t − 9)(t − 1) ≥ 0 0 (t − 1)²(t − 9) ≥ 0 t ∊ <9,∞) U {1} 3^4x ≥ 9 lub 3^4x = 1 4x ≥ 2 lub 4x = 0

	1
x ≥		lub x = 0
	2

	1
x ∊ <		,∞) U {0}
	2

Gustlik: t³ − 11t² + 19t − 9 ≥ 0 Wg mnie prostszy od grupowania jest schemat Hornera − nie trzeba kombinować z podpasowywaniem liczb, samo wszystko wychodzi: 1 −11 19 −9 1 1 −10 9 0 (t − 1)(t² − 10t + 9) ≥ 0 Resztę robisz tak, jak Godzio.

vercia09028: a nie powinno być bez zera, skoro na początku było założenie, że t >0

Godzio: Założenie jest dla t, a nie dla x