pole figury Tomek: Wyznacz pole ograniczone krzywymi y=x² y=10x Więc szukam punktów wspólnych dla prostej i paraboli rozwiązując układ równań z nich złożony, czyli x²=10x x²−10x=0 x(x−10)=0 czyli wspólne punkty to 0 i 10 i nie wiem jak dalej policzyć pole z całki, czy to ma być tak P=∫x²dx−∫10xdx ? oczywiście granica całkowania od 0 do 10 pomoże ktoś ?

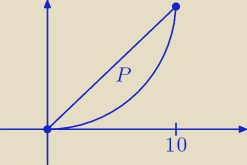
Godzio: Funkcja y = 10x jest powyżej y = x² więc: P = ₀¹⁰∫(10x − x²)dx

Tomek: no tak już w międzyczasie doszedłem do tego sam, tylko zastanawiam się jak będzie dalej czy po

	x3
scałkowaniu to będzie 5x2 −		? i podstawiając pole wyjdzie około 167 ?
	3

Godzio: Tak

ancymon:

	1		x3		x3
∫ (10x−x2) dx = 10 ∫ x dx − ∫ x2 dx = 10*		x2 −		+ C = 5x2 −		+ C
	2		3		3

	103		03		1		2
∫010 (10x−x2) dx = 5*102 −		− 5*02 +		= 500 − 333		= 166
	3		3		3		3