 Zbadaj liczbę rozwiązań równania x2−6|x| +8 =m w zależności od parametru m.
Zbadaj liczbę rozwiązań równania x2−6|x| +8 =m w zależności od parametru m.
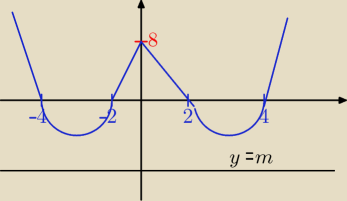
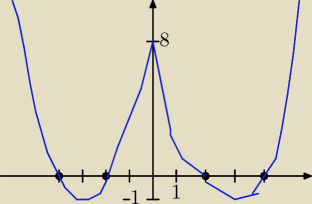 x2 −6IxI + 8 = m
Rozważamy 2 przypadki:
1) Dla x≥0 : x2−6x+8 = m
Δ=4, √Δ=2, x1= 4, x2= 2 (prawa część wykresu)
2) Dla x<0 : x2+6x+8 = m
Δ=4, √Δ=2, x1 = −2, x2 = −4 (lewa część wykresu)
W obu przypadkach współrzędna rzędna wierzchołków parabol jest równa:
x2 −6IxI + 8 = m
Rozważamy 2 przypadki:
1) Dla x≥0 : x2−6x+8 = m
Δ=4, √Δ=2, x1= 4, x2= 2 (prawa część wykresu)
2) Dla x<0 : x2+6x+8 = m
Δ=4, √Δ=2, x1 = −2, x2 = −4 (lewa część wykresu)
W obu przypadkach współrzędna rzędna wierzchołków parabol jest równa:
| −Δ | −4 | |||
q = | = | = −1. | ||
| 4a | 4 |

 te miejsca zerowe sa w końcu na osi pionowej
czy poziomej
te miejsca zerowe sa w końcu na osi pionowej
czy poziomej ?
?
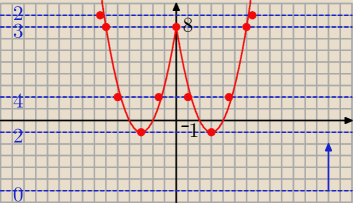 Rysujesz wykres funkcji y=x2−6|x|+8 np. sposobem Anny i teraz metoda "linijkowa".
Bierzesz linijkę lub cokolwiek, co może ją zastąpić, np. ekierkę czy kątomierz, ustawiasz brzeg
linijki poziomo i jedziesz linijka po wykresie wzdłuż osi OY od dołu do góry (przerywana
niebieska linia to linijka, niebieska strzałka pokazuje kierunek przesuwania linijki, a liczby
na poszczególnych liniach ilość rozwiązań). Zatrzymujesz się tam, gdzie linijka dotyka
wierzchołków wykresu oraz wewnątrz przedziałów, np. w miejscach jak na rysunku i liczysz
punkty przecięcia brzegu linijki z wykresem (na rys. to czerwone kropki) − te punkty to
rozwiązania równania.
Odczytujesz po kolei z wykresu wg kolejności przesuwania linijki:
0 rozwiązań dla m∊(−∞, −1)
2 rozwiązania dla m=−1
4 rozwiązania dla m∊(−1, 8)
3 rozwiązania dla m=8
2 rozwiązania dla m∊(8, +∞)
Teraz łączysz ze sobą przypadki z taka samą liczbą rozwiązań i porządkujesz wg liczby
rozwiazań:
0 rozwiązań dla m∊(−∞, −1)
2 rozwiązania dla m∊{−1}U(8, +∞)
3 rozwiązania dla m=8
4 rozwiązania dla m∊(−1, 8)
i masz odpowiedź.
Rysujesz wykres funkcji y=x2−6|x|+8 np. sposobem Anny i teraz metoda "linijkowa".
Bierzesz linijkę lub cokolwiek, co może ją zastąpić, np. ekierkę czy kątomierz, ustawiasz brzeg
linijki poziomo i jedziesz linijka po wykresie wzdłuż osi OY od dołu do góry (przerywana
niebieska linia to linijka, niebieska strzałka pokazuje kierunek przesuwania linijki, a liczby
na poszczególnych liniach ilość rozwiązań). Zatrzymujesz się tam, gdzie linijka dotyka
wierzchołków wykresu oraz wewnątrz przedziałów, np. w miejscach jak na rysunku i liczysz
punkty przecięcia brzegu linijki z wykresem (na rys. to czerwone kropki) − te punkty to
rozwiązania równania.
Odczytujesz po kolei z wykresu wg kolejności przesuwania linijki:
0 rozwiązań dla m∊(−∞, −1)
2 rozwiązania dla m=−1
4 rozwiązania dla m∊(−1, 8)
3 rozwiązania dla m=8
2 rozwiązania dla m∊(8, +∞)
Teraz łączysz ze sobą przypadki z taka samą liczbą rozwiązań i porządkujesz wg liczby
rozwiazań:
0 rozwiązań dla m∊(−∞, −1)
2 rozwiązania dla m∊{−1}U(8, +∞)
3 rozwiązania dla m=8
4 rozwiązania dla m∊(−1, 8)
i masz odpowiedź.