Planimetria - dwa fajne zadanka dla Godzia (i nie tylko) Gustlik: Godzio − dwie łamigłówki dla Ciebie, ale zapraszam także innych 1. (Podobieństwo) W trapezie ABCD (AB||CD, |AB|>|CD|), dwusieczna kąta wewnętrznego o wierzchołku B jest prostopadła do ramienia AD i dzieli je w stosunku 2:1, licząc od wierzchołka A. Oblicz stosunek pola trójkąta powstałego w wyniku podziału trapezu przez tę dwusieczną do pola powstałego czworokąta. 2. Odcinki o długościach 2√3, 3−√3, 3√2 są bokami trójkąta. Oblicz promień okręgu opisanego na tym trójkącie. Dodam, że ja rozwiązałem te zadanka, ale jestem ciekaw, jak Wy sobie z tym poradzicie Miłego rozwiązywania Dodam, że te zadania podyktowała jedna z nauczycielek LO na poziomie... PODSTAWOWYM !

TOmek: 2. Zadanie Policze z tw. cosinusów otrzymam cos= .... −> zamienie to na sin=... i podstawie do wzoru

	a
R=		, dobry pomysł?
	2sin

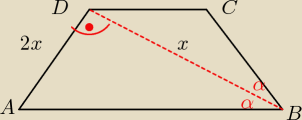TOmek: 1. Dobrze zaznaczyłem dane?

Eta: 2/ R= √6

Gustlik: Dobry pomysł − kontynuuj...

Gustlik: TOmku, ta dwusieczna nie jest przekątną, dzieli ramię AD w stosunku 2:1.

Gustlik: Nieźle, takie zadanka na PODSTAWACH... Chyba się nauczyciele biorą za podnoszenie poziomu matematyki...

TOmek:

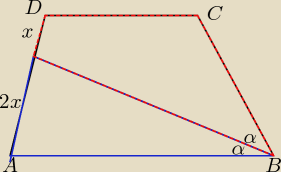
niebieskie
czerwone

no i co dalej : ?

Eta:

	P(Δ)		8
1/ odp:		=
	P(czworokąta)		7

TOmek: how? ide spać , Dobranoc

Eta: TOmek nie poddawaj się , to nie jest takie trudne zadanko

TOmek: jutro sie wezmę, zmęczony dzisiaj jestem ; )

Eta: Ok .... ..... Dobranoc

Godzio: Nadal aktualne ?

Gustlik: Tak, Godzio Fajne zadanka, jak na podstawy, co?

Godzio: Ano fajne, w takim razie zabieram się

Eta:

Godzio: Pierwsze zadanie pamiętam robiłem już z 2 razy I nawet mam arkusz rozszerzony i tam właśnie jest to zadanie, a dokładnie w "Próbnych arkuszach maturalnych" Oficyny Edukacyjnej, więc to zadanie zostawię niech inni myślą, ale drugie chętnie zrobię

Gustlik: No właśnie chciałem, zebyś zrobił to pierwsze, jeśli możesz, bo jestem ciekaw metody, jaką wybierzesz. Mi wyszło dobrze, mam taki sam wynik jak Eta. Robiłem to zadanie dzisiaj z uczennicą na podstawach.

Eta: He he.... drugie jest proste jak .... barszcz

Gustlik: Drugie jest proste, pierwsze też fajne, tylko jestem ciekaw metody na to pierwsze. Wynik mi

	8
wyszedł		, więc jest dobrze.
	7

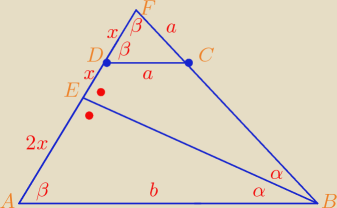Godzio: Ja tak to zrobiłem: Trójkąty ABE i BEF są przystające (k,b,k) Więc |ED| = |DF| = x Z podobieństwa DCF i ABF:

a		x		a		1
	=		⇒		=		⇒ b = 4a
b		4x		b		4

	2x
sinα =		⇒ 2x = sinα * b
	b

	1		1
P1 =		* 2x * b * sinβ =		b2sinαsinβ = 8a2sinαsinβ
	2		2

	1
P2 =		axsinβ = a2sinαsinβ
	2

P₃ = P₁ − P₂ = 8a²sinαsinβ − a²sinαsinβ = 7a²sinαsinβ

P1		8
	=
P3		7

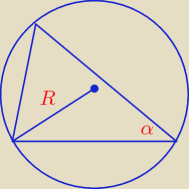Godzio: 2√3, 3−√3, 3√2 Z twierdzenia cosinusów: 12 − 6√3 = 12 + 18 − 12√6cosα 12√6cosα = 18 + 6√3

	18 − 6√3		(3 − √3)√6
cosα =		=
	12√6		12

	(12 − 6√3) * 6		2 − √3
cos2α =		=
	12 * 12		4

	2 + √3
sin2α = 1 − cos2α =
	4

	12 − 6√3		48 − 24√3
4R2 =		=		= 96 + 48√3 − 48√3 − 72
	sin2α		2 + √3

4R² = 24 2R = 2√6 R = √6

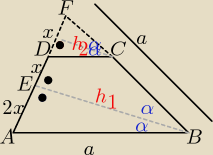Eta: ΔABE ~ ΔBEF ( bo są prostokatne i mają kąt α zatem |EF| = |AE| = 2x i |AB|= BF|= a i |ED|= |DF|= x

	4x
ΔABF ~ ΔDCF w skali k=		= 4
	x

zatem h₁= 4*h₂ P(ΔABE) = x*h₁ = 4x*h₂

	1
P(ΔDCF)=		*x*h2
	2

	1		1
P( czworokąta BECD)= P(ΔEBF) − P(ΔDCF)= x*h1 −		*x*h2= 4*xh2−		x*h2=
	2		2

	7
=		*x*h2
	2

	P(ΔABE)		4*xh2		8
i teraz:		=		=
	P(EBCD)		7   *xh2 2		7

Godzio: Jest jakiś łatwiejszy sposób na rozwiązanie tego drugiego zadania ?

Eta: W pierwszym zapisie ma być ( trójkąty przystające ! a Godzio ... "kocha" trygonometrię

Godzio:

Gustlik: Eta, Twój sposób nieco podobny do mojego. Pozdrawiam

Gustlik: Niemniej ciekawe zadania, jak na poziom podstawowy.

Bogdan:

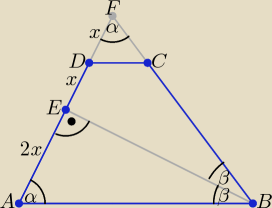
	4x		PABF
Trójkąty ABF i DCF są podobne w skali		= 4 ⇒		= 16
	1x		PDCF

PABE		PABE
	=		=
PEBCD		PEBF − PDCF

1   PABF   2		16
	*		=
1   1   PABF − PABF 2   16		16

	8PABF		8
=		=
	7PABF		7

Gustlik: Też fajny sposób, pozdrawiam Bogdan

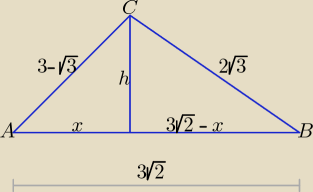Bogdan: Zadanie 2 można na poziomie podstawowym rozwiązać np tak: h² + 18 − 6√2x +x² = 12 h² + x² = 9 − 6√3 + 3 (*) − −−−−−−−−−−−−−−−−−−−−−−

	3−√3		12−6√3
18 − 6√2x = 6√6 ⇒ x =		⇒ x2 =		= 6−3√3
	√2		2

(*) h² = 12 − 6√3 − x² = 12 − 6√3 − 6 + 3√3 = 6 − 3√3 = x² ⇒ h = x

	1		3−√3		9 − 3√3
PABC =		*3√2*		=
	2		√2		2

	(3−√3) * 2√3 * 3√2		(3−√3) * 6√6
R =		=		= √6
	9−3√3   4 *   2		2*3(3−√3

	abc
Długość promienia okręgu opisanego na trójkącie wyznaczyłem z zależności: R =
	4PΔ

Bogdan: Również pozdrawiam Ciebie Gustliku , zadania podobały mi się.