Wielomiany
Ewa: Umie ktoś rozwiązać takie wielomiany? proszę o pomoc
Sprawdź która z licz z podanego zbioru A= { −1, √2, 3 } jest pierwiastkiem wielomianu
W(x) = x3 − 3x2 − 4x + 12
Wyznacz wartośc parametru a tak, aby liczba p = −1 była pierwiastkiem wielomianu
W(x) = x5 +ax4 + x2−x
Wyznacz warośc parametru k, dla którego wielomian W(x) = −2x4 + kx2 − (3k−2)x + 4 jest
podzielny przez dwumian x+1
Wykaż że liczba r = −2 jest pierwiastkiem W(x) = x3 − x2 − 16x − 20 a następnie oblicz
pozostałe pierwiastki wielomianu
Powie mi ktoś jak to rozwiązać?
22 maj 20:34
dooominisia: 1)
w(x)=x2(x−3)−4(x−3)
w(x)=(x2−4)(x−3)
w(x)=(x−2)(x+2)(x−3)
x=2, x=−2, x=3
2)w(−1)=0
w(−1)=−1+a+1+1
2−1+a=o
1+a=o
a=−1
22 maj 21:54
dooominisia:
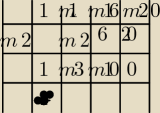
3)w(−2)=−8−4+32−20=0
Teraz należy w(x):(x+2) →pisemnie lub schemat hornera( podajże), wynik który otrzymam to:
x
2−3x−10=p(x)
Mogę zapisać:
w(x)=p(x)*(x+2)
Należy obliczyć deltę, pierwiastki do wzoru p(x)→miejsca zerowe
trzecim miejscem zerowym jest x=−2
*w rysunku przed liczbami m znaczy że liczba jest na minusie
22 maj 22:04
Gustlik: ad 3) Wyznacz warośc parametru k, dla którego wielomian W(x) = −2x4 + kx2 − (3k−2)x + 4 jest
podzielny przez dwumian x+1
Z twierdzenia Bezout mamy: W(−1)=0. Dalej robisz jak zad. 2 − tak, jak zrobiła
dooominisia.
23 maj 00:21
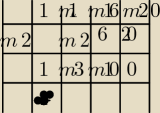 3)w(−2)=−8−4+32−20=0
Teraz należy w(x):(x+2) →pisemnie lub schemat hornera( podajże), wynik który otrzymam to:
x2−3x−10=p(x)
Mogę zapisać:
w(x)=p(x)*(x+2)
Należy obliczyć deltę, pierwiastki do wzoru p(x)→miejsca zerowe
trzecim miejscem zerowym jest x=−2
*w rysunku przed liczbami m znaczy że liczba jest na minusie
3)w(−2)=−8−4+32−20=0
Teraz należy w(x):(x+2) →pisemnie lub schemat hornera( podajże), wynik który otrzymam to:
x2−3x−10=p(x)
Mogę zapisać:
w(x)=p(x)*(x+2)
Należy obliczyć deltę, pierwiastki do wzoru p(x)→miejsca zerowe
trzecim miejscem zerowym jest x=−2
*w rysunku przed liczbami m znaczy że liczba jest na minusie