Równanie z wartością bezwzględną Pepsi2092: Równanie z wartością bezwzględną: |x+1| − |x|=0 jak ktoś może to prosze o udzielenie wskazówek.

Dziaku: Robisz dwa przypadki dla x≥0 oraz x<0

Pepsi2092: No czaje, że korzystam z definicji wartosci bezwzględnej, ale jak 2 tylko przypadki jak jeszcze jest |x+1| to chyba 4 przypadki jak już coś, ale myślałem ,że da się jakoś to na skróty obejść tak jak w równaniach typu |x−2|+|x+2|=4 , wyznaczasz miejsca zerowe i ciśniesz na przedziałach a potem suma ze wszystkich rozwiazań i po wszystkim.

bart: robisz trzy przypadki x∊(−∞,−1) u <−1,0) u <0,+∞)

bart: lub.. |x+1|=|x| hmmm..?

Pepsi2092: Ok Dzięki wielkie bart, czyli tam gdzie |x| przyjmuję, że miejsce zerowe jest 0?

bart: tak

bart: |x+1|=|x| przemysl to

Pepsi2092: Ja Ci zrobie jak to po mojemu powinno wygladać a Ty sprawdzisz mi najwyzej

Pepsi2092: |x+1| − |x|=0 Miejsca zerowe to: −1,0 , w obu przypadkach funkcja jest rosnąca bo x jest dodatni, zatem rozwiązuję równanie w 3 przedziałach: (−∞,−1) ; <−1,0) ; <0,∞). 1.(−∞,−1) x+1<0 , więc |x+1|= −x−1 x<0, więc |x|= −x |x+1| − |x|=0 −x−1+x=0 −1≠0 −− sprzeczne, wiec nie ma rozwiazań w tym przedziale, x∊∅ 2.<−1,0) x+1≥0, więc |x+1|= (x+1) x<0, więc |x|= −x |x+1| − |x|=0 x+1+x=0 2x=−1||\2

	1		1
x=−		− spełnia warunek i liczba x=−		jest rozwiązaniem równania w tym
	2		2

przedziale. 3.<0,∞) x+1>0, więc |x+1|= (x+1) x≥0, więc |x|= x |x+1| − |x|=0 x+1−x=0 1≠0 sprzeczne, czyli w tym przedziale x∊∅

	1
Zatem rozwiązanie tego równania to suma rozwiazań z 1,2,3 , więc tylko liczba −		jest
	2

rozwiazaniem |x+1| − |x|=0. Myślę, że tak ale sprawdź bart jak możesz

bart: no pasuje

Grześ: brawo... sposób taki naokoło, że hej.. jest o wiele szybszy, który bart chyba sugerował, nie jestem pewny. Korzystamy z zależności, że jeśli mamy: |a|=|b|, to wtedy: a=b lub a=−b czyli: |x+1|=|x| x+1=x lub x+1=−x 1=0 2x=−1, czyli x=−1/2 sprzeczne

hrthrthtrht: Ω∞∫→⇒

i tyle:

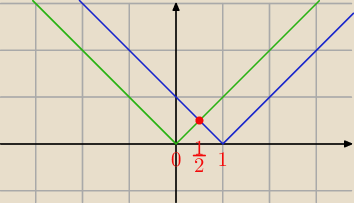
	1
|x − 1| = |x| ⇒ x =		i tyle
	2

Mila: |x+1| − |x|=0 ⇔ |x+1|=|x| /² ( obie strony są dodatnie.) x²+2x+1=x² 2x=−1

	−1
x=
	2