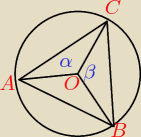
fggfh pysia1993: Trójkąt ABC jest wpisany w okrąg o środku O. Mając AB = c oraz kąty α i β zaznaczone na rysunku, znajdź AC = b i BC = a

Godzio: Z twierdzenia cosinusów w trójkącie ABO: c² = R² + R² − 2R²cos(180 − (α + β) ) c² = 2R² + 2R²cos(α + β) c² = 2R²(1 + cos(α + β) )

	c2
2R2 =
	1 + cos(α + β)

Teraz w trójkącie BCO : a² = 2R² − 2R²cosβ

	c2		c2cosβ
a2 =		−
	1 + cos(α + β)		1 + cos(α + β)

	c2(1 − cosβ)
a2 =
	1 + cos(α + β)

	c√1 − cosβ
a =
	√1 + cos(α + β)

Analogicznie wylicz b

Godzio: [P[Anna] rozwiązała prościej więc na moje rozwiązanie nie patrz pomijając że powinno być 360 − (α + β) i wtedy znak cosinusa się nie zmienia

pysia1993: Dobrze. dzieki wielkie za pomoc.

pysia1993: A umiesz takie zadanie.: W trojkacie ABC dane sa BC = a i katy beta i gama. Wyznacz dlugosci odcinkow wycietych z dwusiecznych tego trojkata przez jego brzeg.?! z gory dziekuje za pomoc.

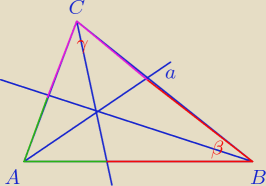
Godzio: To chyba o ten odcinki chodzi hmmm, masz do tego odp ? Wyliczę i się sprawdzi

pysia1993: Wlasnie kurde nie ma odpowiedzi. bo dal nam na kartce wydrukowane zadania...

Godzio: Ten czerwony odcinek wyszedł mi:

γ   asin   2		1   asinγcos( (γ + β))   2
	+
γ   sin( +β)   2		1   sin(β + γ)cos( (γ − β))   2

Więc chyba nie o to chodzi

pysia1993: Ja nie mam pojecia... wgl nie czaje tych zadan...