Pomocy!!!! Funkcja kwadratowa: Napisz wzór funkcji kwadratowej f, o której wiadomo, że; a) jednym z miejsc zerowych jest liczba 2, największa jej wartość jest równa 5 i jest ona malejąca w przedziale <3,+∞) ,a rosnąca w przedziale (−∞, 3>, b) suma miejsc zerowych jest rowna 8, a suma odwrotnści miejsc zerowych jest rowna 2/3 oraz f(0)=24 c) f(1)= 0 i a najmniejszą wartość funkcja f ma dla argumentu x=−1 , a wykres funkcji przechodzi przez punkt o współrzędnych (2,5) d) przedział<2 + ∞) jest maxymalnym przedzialem, w którym funkcja jest malejąca, a w przedziale <−8;−7> ma największą wartość y max= −24 oraz jednym z miejsc zerowych jest liczba 5, e) wyraz wolny c= 5 oraz zacjodzi równość f(x+1)−f(x)−8x=3 , gdy xε R f) miejscami zerowymi są liczby ! oraz ₃ i wykresem jest parabola styczna do prostej o równaniu y=−4 PROSZĘ O POMOC W ROZWIĄZANIU CHOCIAZ JEDNEGO PODPUNKTU NAPROWADZENIE NA ROZWIĄZANIE NAPRAWDĘ NIE WIEM JAK TO ZROBIĆ POMOCY DZIĘKI Z GÓRY TYM KTÓRZY CHCA MI POMÓC

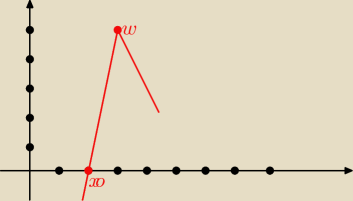
dooominisia: odnośnie podpunktu a w 2 miejsce zerowe największa wartość =3→x wierzchołkowe=3, a y wierzchołkowe możemy odczytać z informacji o przedziałach w których funkcja jest rosnąca i malejąca, więc W(3,5) Równanie w którym a<0 ma posatć: ax²+bx+c=f(x) Musimy teraz ułożyć trzy równania: f(2)=0 f(3)=5 (i ze wzorów na x wierzchołkowe): −b/2a=3 Trzeba rozwiążać układ równań tzn. wyznaczyć z trzeciego równania b i podstawić do pierwszego i drugiego równania. Otzrymamy: a=−5 b=30 c=−40

dooominisia: b)Równanie również ma postać: ax²+bx+c=f(x) nazleży skorzystać ze wzorów Vitae: x1+x2=−b/a x1*x2=c/a Układamy układ równań: Pierwsze równanie: x1+x2=8 Więc: −b/a=8 Drugie równanie trzeba przekształcić: 1/x1+1/x2=2/3 1/x1+1/x2=(x2/(x1*x2))+(x1/(xa*x2))=(x1+x2)/(x1*x2)→mam nadzieję ze dzięki nawiasom będzie bardzoej czytelne Więc drugie równanie ma postać: (x1+x2)/(x1*x2)=2/3 −b/a:c/a=−b/a*a/c=−b/c Więc: −b/c=2/3 I ostatnie równanie układamy na podstawie informacji: f(0)=24, więc a*0+b*o+c=24 więc c=24 Należy również rozwiązać układ równań i podstawić do ax²+bx+c=f(x)

dooominisia: c) również układ równań: f(1)=0 −b/2a=−1 f(2)=5 Więc: a+b+c=0 b=2a 4a+2b+c=5 Należy podstawić do pierwszego i tzreciego równania drugie równanie i powinno wyjść

;): a) x_w = 3 y_w = 5 x₁ = 2 6 = 2 + x₂ x² = 4 f(x) = a(x − 2)(x − 4) −a = 5 a = −5 f(x) = −5(x − 2)(x − 4)

FUNKCAJA: DZIĘKUJĘ

maniek: 5² elo

Krzysiek: Zapytaj siostrzenca z podstawowki

Eta: tyle co 9^log₃5