Potrzebuje pomocy z obliczeniem pochodnych!!!
Kajol:
1) f(x)=e
x*cos
2x
2) f(x)=
√sinx+√x+2√x
3) f(x)=e
cosx
4) f(x)=2
3x
5) f(x)=(4x
2−5x+13)
5/3
Proszę o rozwiązanie z wytłumaczeniem co i jak po kolei. Z góry dziękuję

.
20 maj 14:45
Jack:
próbowałeś sam?

Napisz swoje rozwiązania
20 maj 14:58
Kajol: Hej nie nie próbowałam, bo nie wiem o co chodzi. Pan na zajęciach nam tego nie wytłumaczył.
Wiem, że trzeba najpierw znaleźć pochodne wszystkich tych funkcji i na tym koniec...
20 maj 15:00
Kajol: Sorry to nie to zadanie

. Przed chwila dodałam inne. Zaraz napiszę.
20 maj 15:00
Godzio:
1. (e
x)' = e
x (cos
2x)' = −2cosx * sinx = −sin2x (f * g)' = f' * g + f * g'
(e
x * cos
2x)' = (e
x) * cos
2x + e
x * (cos
2x)' = e
x(cos
2x − sin2x)
3. (cosx)' = −sinx
(e
cosx)' = e
cosx * (−sinx) = −e
cosx * sinx
4. (2
3x)' = (e
ln23x)' = (e
3x * ln2)' = e
3x * ln2 * ln2 * 3
x * ln3 =
= 2
3x * 3
x * ln2 * ln3
5. (x
n)' = n * x
n − 1 (f(y))' = f '(y) * y'
| | 5 | |
((4x2 − 5x + 13)5/3)' = |
| (4x2 − 5x + 13)2/3 * (8x − 5) |
| | 3 | |
20 maj 15:03
Kajol:
1) f(x)'=e
x*cos
2x−sin
2x*e
x
2) Tu się totalnie zagmatwałam. Niby wyliczyłam wszystkie po kolei, ale nie umiem zapisać
rozwiązania.
3) f(x)'= e
cosx*(−sinx*lne
cosx−sinx*cosx)
Do lego przykładu mam pytanie. Czy lne
cosx to to samo co cosx*lne

? I czy lne=1

?
4) Tego nawet nie ruszyłam...
5) f(x)'=(4x
2−5x+13)
5/3*[
53*ln(4x
2−5x+13)]'=
(4x
2−5x+13)
5/3*[
53*(ln4x
2−ln5x+ln13)
20 maj 15:13
Kajol: Dziękuję Godzio, ale rozwiązania do 5 przykładu nie rozumiem...
20 maj 15:16
Ajtek: W 5 masz pochodną wewnętrzną z nawiasu.
20 maj 15:18
Ajtek: (4x2−5x+13)'=8x−5
20 maj 15:19
Godzio:
Tutaj masz funkcję złożoną, funkcją zewnętrzną jest (...)
5/3 i liczysz to tak samo jak każdą
inną funkcję z jakąś pochodną.
| | 5 | |
( (...)5/3 )' = |
| (...) * (...)' |
| | 3 | |
20 maj 15:19
Ajtek: Pięknie wyłożone
Godzio 
.
20 maj 15:20
Kajol: Aha no tak. Dzięki wielkie

. Teraz to naprawdę jest łatwe

.
Aha i jeszcze jedno na serio tylko tyle wystarczyło zrobić w przykładzie 2

? Ja zrobiłam go za
pomocą wzoru, który podam mi wykładowca...
20 maj 15:21
Godzio: 
20 maj 15:21
Godzio:
2 Ci nie powiem bo nie wiem co tam dokładnie jest : D
20 maj 15:22
Kajol:
A wzór wygląda tak: f(x)=g(x)h(x)
f(x)'=f(x)*[h(x)*ln g(x)]'=f(x)*[ln f(x)]'
20 maj 15:24
Ajtek: Zaczynam przypominać sobie pochodne

.
20 maj 15:24
Godzio:
To chyba o trzecim mówiłaś, takiego wzoru nie znałem

20 maj 15:25
Kajol: To znaczy o co dokładnie chodzi

?
20 maj 15:26
Kajol: A tak o 3
20 maj 15:26
Kajol: No a ja właśnie wg niego robię funkcje, które są do potęgi. Tak mam na liście... Ale to co
zrobiłeś jest poprawne prawda

? Nie trzeba było tak tego gmatwać jak ja

?
20 maj 15:27
Godzio:
No to jest ok, źle chyba go zastosowałaś:
lnecosx = cosx
lne = 1
Więc jak masz
f'(x) = f(x) * [ lnf(x) ]' To patrząc na funkcję:
(ecosx)' = ecosx * (lnecosx)' = ecosx * (cosx)' = −ecosxsinx
20 maj 15:28
Godzio:
Nie trzeba, nie trzeba

20 maj 15:28
Kajol: A o co chodzi z 2

Tam są 3 pierwiastki. Jeden nad całym działaniem. Drugi po pierwszym +. A trzeci nad ostatnim
x.
20 maj 15:29
Godzio:
Jak masz e.... to liczysz pochodną tak:
(ef(x))' = ef(x) * (f(x))' I dalej liczysz odpowiednią pochodną do danej funkcji
20 maj 15:29
Kajol: Aha no spoko. Właśnie nie byłam pewna czy lne=1. Teraz już mam potwierdzenie

. Dziękuję

. A
ten 2 tez zrobisz

Proszę

!
20 maj 15:31
Godzio:
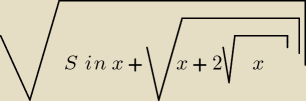
Tak wygląda ?
20 maj 15:32
Kajol: Ok będę pamiętać

.
20 maj 15:32
Godzio:
(
√sinx + √x + 2√x)' =
| 1 | | 1 | | 2 | |
| * (cosx + |
| * (1 + |
| ) ) = |
| 2√sinx + √x + 2√x | | 2√x + 2√x | | 2√x | |
| 1 | | 1 | | 1 | |
| * (cosx + |
| * (1 + |
| ) ) |
| 2√sinx + √x + 2√x | | 2√x + 2√x | | √x | |
Upraszczać już mi się nie chce, jak chcesz to to zrób
20 maj 15:38
Kajol: Dokładnie tak

20 maj 15:52
Kajol: Ok ale skąd się to wszystko wzięło

? Ta 2 w mianowniku i w ogóle

? Dziękuje.
20 maj 15:54
Godzio:
| | 1 | |
(√...)' = |
| * (...)' |
| | 2√... | |
I tak dopóki Ci się nie skończy
20 maj 15:54
Kajol: Aha dziękuję Ci bardzo

. Będę o tym pamiętać

.
20 maj 15:56
Kajol: A i jeszcze jedno skąd się wzięło 2 w liczniku

?
20 maj 15:58
Godzio:
| | 1 | | 2 | | 1 | |
(2√x)' = 2 * (√x)' = 2 * |
| = |
| = |
| |
| | 2√x | | 2√x | | √x | |
20 maj 16:02
Kajol: Ok dziękuję za pomoc. 3maj się ciepło

.
20 maj 16:09
Kajol: Mam pytanko do 1 przykładu. Czemu −2cosx * sinx = −sin2x

20 maj 18:35
voltage: 2sinxcosx=sin2x, więc
−2sinxcosx=−sin2x
20 maj 19:19
Kajol: Aha wielkie dzięki

.
21 maj 13:31
Kajol: Hej. Mam jeszcze taką funkcję:
f(x)=ln(tgx)
czy pochodna wygląda tak:
| | 1 | |
Znalazłam we wzorach na pochodne, że (tgx)'= |
| |
| | cos2x | |
21 maj 14:15
Godzio:
Jest ok
21 maj 14:24
Kajol: No to ekstra


Bardzo Ci dziękuję za pomoc

. I całej reszcie osób piszących również

.
3majcie się ciepło

.
21 maj 18:12
 .
.
 Napisz swoje rozwiązania
Napisz swoje rozwiązania
 . Przed chwila dodałam inne. Zaraz napiszę.
. Przed chwila dodałam inne. Zaraz napiszę.
 ? I czy lne=1
? I czy lne=1  ?
4) Tego nawet nie ruszyłam...
5) f(x)'=(4x2−5x+13)5/3*[53*ln(4x2−5x+13)]'=
(4x2−5x+13)5/3*[53*(ln4x2−ln5x+ln13)
?
4) Tego nawet nie ruszyłam...
5) f(x)'=(4x2−5x+13)5/3*[53*ln(4x2−5x+13)]'=
(4x2−5x+13)5/3*[53*(ln4x2−ln5x+ln13)
 .
.
 . Teraz to naprawdę jest łatwe
. Teraz to naprawdę jest łatwe .
Aha i jeszcze jedno na serio tylko tyle wystarczyło zrobić w przykładzie 2
.
Aha i jeszcze jedno na serio tylko tyle wystarczyło zrobić w przykładzie 2 ? Ja zrobiłam go za
pomocą wzoru, który podam mi wykładowca...
? Ja zrobiłam go za
pomocą wzoru, który podam mi wykładowca...

 .
.

 ?
?
 ? Nie trzeba było tak tego gmatwać jak ja
? Nie trzeba było tak tego gmatwać jak ja ?
?

 Tam są 3 pierwiastki. Jeden nad całym działaniem. Drugi po pierwszym +. A trzeci nad ostatnim
x.
Tam są 3 pierwiastki. Jeden nad całym działaniem. Drugi po pierwszym +. A trzeci nad ostatnim
x.
 . Dziękuję
. Dziękuję . A
ten 2 tez zrobisz
. A
ten 2 tez zrobisz Proszę
Proszę !
!
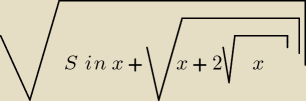 Tak wygląda ?
Tak wygląda ?
 .
.

 ? Ta 2 w mianowniku i w ogóle
? Ta 2 w mianowniku i w ogóle ? Dziękuje.
? Dziękuje.
 . Będę o tym pamiętać
. Będę o tym pamiętać .
.
 ?
?

 .
.

 .
.


 Bardzo Ci dziękuję za pomoc
Bardzo Ci dziękuję za pomoc . I całej reszcie osób piszących również
. I całej reszcie osób piszących również .
3majcie się ciepło
.
3majcie się ciepło .
.