 WIEM, ŻE DUŻO NAPISANE, ALE BŁAGAM POMÓŻCIE
Kompletnie nie czaje funkcji, dlatego zgłaszam się do was jak narazie
WIEM, ŻE DUŻO NAPISANE, ALE BŁAGAM POMÓŻCIE
Kompletnie nie czaje funkcji, dlatego zgłaszam się do was jak narazie  Mam zadanie z funkcją. Muszę narysować funkcję i podać jej własności. Funkcja ta to: y = U{ 3
}{ x+1 } −2. Tabelke zrobiłam, wychodzi mi, że jak x jest 0 to, y 1, jak x jest 1 to y U{ 1 }{
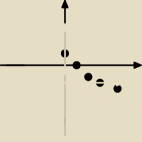
2 }, jak x 2 to y to −1 itd. Wykres mam narysowany, raczej dobrze. I teraz pojawiają się
problemy. Najpierw w ogóle ta funkcja ma jakąś nazwę? (sory za durne pytanie, ale naprawdę nie
czaje) na pewno nie kwadratowa, ale to jaka, wymierna? czy po prostu funkcja wzoru f(x)=U{ a
}{ x−p } +q?
Mam zadanie z funkcją. Muszę narysować funkcję i podać jej własności. Funkcja ta to: y = U{ 3
}{ x+1 } −2. Tabelke zrobiłam, wychodzi mi, że jak x jest 0 to, y 1, jak x jest 1 to y U{ 1 }{
2 }, jak x 2 to y to −1 itd. Wykres mam narysowany, raczej dobrze. I teraz pojawiają się
problemy. Najpierw w ogóle ta funkcja ma jakąś nazwę? (sory za durne pytanie, ale naprawdę nie
czaje) na pewno nie kwadratowa, ale to jaka, wymierna? czy po prostu funkcja wzoru f(x)=U{ a
}{ x−p } +q?
| 1 | ||
I np miejsce zerowe, na osi wygląda na | a z obliczen 0. Chyba jest to funkcja | |
| 2 |
 No i wykres u mnie wygląda jakoś tak, jak narysowałam wyżej.
No i wykres u mnie wygląda jakoś tak, jak narysowałam wyżej.
| 1 | ||
Wiesz jak wygląda wykres funkcji y= | ? | |
| x |
| 3 | 3 | |||
różnią. A Twój wykres y= | −2, to jest właśnie wykres y= | , przesunięty o wektor | ||
| x+1 | x |
 Mój błąd
Mój błąd

 to mam dobrze ten wykres narysowany czy ma byc taki jak z
linku? I co to znaczy przesunięty o wektor i czemu też jest przesunięty o −1? A miejsce
zerowe, to 0 czy 1/2 czy w ogole nie ma? Sory, ale z funkcji jestem tępa
to mam dobrze ten wykres narysowany czy ma byc taki jak z
linku? I co to znaczy przesunięty o wektor i czemu też jest przesunięty o −1? A miejsce
zerowe, to 0 czy 1/2 czy w ogole nie ma? Sory, ale z funkcji jestem tępa 
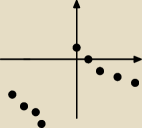 Czyli to będzie coś takiego? Powiedzmy, bo jak np. x jest −2 to y −5, jak x −3 to y −3,5. W
takim razie co z miejscem zerowym? a dziedzina to −1, co nie?
Czyli to będzie coś takiego? Powiedzmy, bo jak np. x jest −2 to y −5, jak x −3 to y −3,5. W
takim razie co z miejscem zerowym? a dziedzina to −1, co nie? 
| 3 | ||
wykres | przesuwasz o 1 jednostkę w lewo i 2 jednostki w dół. | |
| x |
| 3 | 3 | |||
Przesunięty jest dlatego, że jak widzisz nie jest to samo y= | , tylko y= | −2 | ||
| x | x+1 |
| c | ||
Wzór ogólny to y= | +q , c− dowolna liczba całkowita. W takim przypadku przesuwasz | |
| x−p |

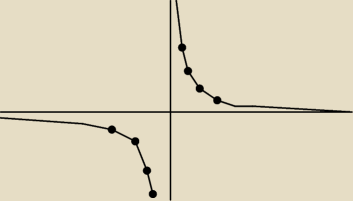
| 3 | ||
To jest y= | ||
| x |
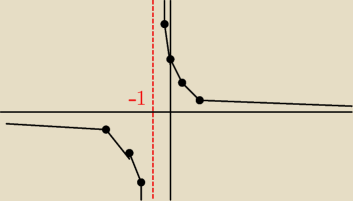 Dobra najpierw przesunąłem o wektor [−1,0]
Dobra najpierw przesunąłem o wektor [−1,0]
| 3 | ||
Ta funkcja ma wzór y= | ||
| x+1 |
| 3 | ||
A ma być y= | −2, czyli ten wykres trzeba opuścić o 2 jednostki w dół jeszcze.  | |
| x+1 |

| 3 | ||
I oto nasz oczekiwany od początku wykres y= | −2 | |
| x+1 |



| 3 | ||
Ok, ale jak sie oblicza dziedzine funkcji z tego y = | − 2 ? | |
| x + 1 |
| 1 | ||
A miejsce zerowe to | prawda? | |
| 2 |
 Jeszcze sa jakies wlasnosci?
Ja wiem, ze moze pytam o proste rzeczy, ale to juz ostatnie
Jeszcze sa jakies wlasnosci?
Ja wiem, ze moze pytam o proste rzeczy, ale to juz ostatnie 
 Miejsce zerowe też się zgadza.
Zbiór wartości są to wszystkie wartości ( igreki
Miejsce zerowe też się zgadza.
Zbiór wartości są to wszystkie wartości ( igreki  ), które funkcja może osiągnąć, zauważ że
ta funkcja osiąga wszystkie wartości oprócz −2, dlatego zbiór wartości to y∊R\{−2}.
Co do monotoniczności, to znowu patrzysz na wykres i określasz monotoniczność. W tym przypadku
jest to funkcja malejąca, gdyż wraz ze wzrostem argumentów, wartości maleją w przedziałach
(−∞,−1) i (1,∞).
Co do własności, to by się jakieś pewnie jeszcze znalazły (chociażby ekstrema, tutaj ich nie
ma), ale w tej funkcji myślę że to raczej wystarczy.
), które funkcja może osiągnąć, zauważ że
ta funkcja osiąga wszystkie wartości oprócz −2, dlatego zbiór wartości to y∊R\{−2}.
Co do monotoniczności, to znowu patrzysz na wykres i określasz monotoniczność. W tym przypadku
jest to funkcja malejąca, gdyż wraz ze wzrostem argumentów, wartości maleją w przedziałach
(−∞,−1) i (1,∞).
Co do własności, to by się jakieś pewnie jeszcze znalazły (chociażby ekstrema, tutaj ich nie
ma), ale w tej funkcji myślę że to raczej wystarczy. 
