planimetria
olkaaa: Miara największego kąta w trójkącie jest 2 razy większa od miary najmniejszego. Oblicz długość
boków tego trójkąta, jeżeli są one kolejnymi liczbami naturalnymi.
Proszę o wytłumaczenie, jak to zrobić

19 maj 20:13
olkaaa: nikt? bo ja to nie wiem jak się robi zadania "praktycznie bez danych"
19 maj 21:31
Eta:
Pomogę

..... rysuję .... cierpliwości
19 maj 21:34
olkaaa: dzięki

19 maj 21:37
Eta:
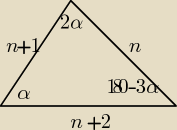
α −−− miara kąta najmniejszego, to naprzeciw kąta α leży najkrótszy bok dł. n
2α −− miara kata największego, to naprzeciw niego leży najdłuższy bok dł. n+2
180
o −3α −−−leży bok dł. n+1
1/ ze wzoru sinusów
| | n | | n+2 | | n+2 | |
|
| = |
| = |
|
|
| | sinα | | sin2α | | 2sinα*cosα | |
| | n+2 | |
po przekształceniu otrzymujemy: cosα= |
|
|
| | 2n | |
teraz ze wzoru cosinusów
| | (n+1)2+ (n+2)2 −n2 | |
cosα= |
|
|
| | 2*(n+1)*(n+2) | |
po wykonaniu działań otrzymasz:
| | n2+6n+5 | | (n+1)(n+5) | | n+5 | |
cosα= |
| = |
| = |
|
|
| | 2(n+1)(n+2) | | 2(n+1)(n+2) | | 2(n+2) | |
porównując cosinusy
rozwiazujac to równanie otrzymasz n= 4
zatem boki maja długości:
4, 5, 6

19 maj 21:47
;): 

19 maj 21:53
olkaaa: z 20 minut myślałam jak przekształciłaś/eś wzór o twierdzeniu cosinusów... a to był taki
banał, no ale cóż, noga matematyczna jestem. wielkie dzięki!
19 maj 23:17
19 maj 23:30
olkaaa: okey, dzięki, na lekcji były zadania z łatwymi danymi, więc na samym końcu dało się wyliczyć
cosinus, a że z przekształcania jestem słaba, to się trochę teraz pomęczyłam

19 maj 23:45
faradaja: mam pytanie, dlaczego jeżeli najpierw cosa wylicze z tw. cosinusow a potem wstawie do tw.
sinusow to nie wychodzi?
1 kwi 15:46
faradaja: już wiem, zapomniałam o współczynniku po rozłożeniu kwadratu na nawiasy

1 kwi 15:49

 ..... rysuję .... cierpliwości
..... rysuję .... cierpliwości

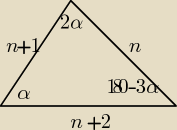 α −−− miara kąta najmniejszego, to naprzeciw kąta α leży najkrótszy bok dł. n
2α −− miara kata największego, to naprzeciw niego leży najdłuższy bok dł. n+2
180o −3α −−−leży bok dł. n+1
1/ ze wzoru sinusów
α −−− miara kąta najmniejszego, to naprzeciw kąta α leży najkrótszy bok dł. n
2α −− miara kata największego, to naprzeciw niego leży najdłuższy bok dł. n+2
180o −3α −−−leży bok dł. n+1
1/ ze wzoru sinusów




