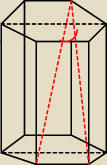
Oblicz wysokość o objętość graniastosłupa. Premier: W graniastosłupie prawidłowym sześciokątnym krótsza i dłuższa przekątna wychodzące z tego

	12
samego wierzchołka (patrz rysunek) tworzą kąt którego cosinus jest równy		. Krawędź
	13

podstawy ma 10cm długości. Oblicz wysokość o objętość graniastosłupa.

asd: jak narazie doszedłem do tego że sinus tego kąta to ⁵₁₃ spróbuję pomyśleć coś jeszcze

asd: Zakładając że ten trójkąt jest prostokątny to jego naprzeciwprostokątna(dłuższa przekątna) mamy równanie ⁵₁₃ = ¹⁰_x x=26 dłuższa przekątna 26²= 100+y² 676−100= y² y=24

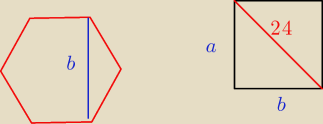
asd: Ok to jest prostokąt ktorego przekątna jest też krótszą przekątną. Jego b równe jest 10√3 a²+b²=24² 576= 300+276 a²= 276 a= 2√69 Pp= 150√3 V= 150√3*2√69 V= 300√207 co mi tu wyszło? o.O