AS:
Dowód metodą analityczną
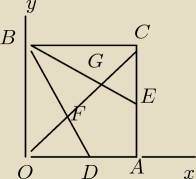
Przyjąłem bok kwadratu OA = a. Wtedy
O(0,0) , A(a,0) , B(0,a) , C(a,a) , D(a/2,0) , E(a,a/2)
Równania prostych:
OC: y − 0 = (a − 0)/(a − 0)*(x − 0) ⇒ y = x
BD: y − a = (0 − a)/(a − a/2)*(x − a) ⇒ y = −2*x + a
BE: y − a = (0 − a/2)/(a − 0)*(x − 0) ⇒ y = a − x/2
Punkty przecięcia prostych
Punkt F − rozwiązuję układ równań
y = x
y = −2*x + a rozwiązaniem: x = a/3 , y = a/3 , F(a/3,a/3)
Punkt G rozwiązuję układ równań
y = x
y = a − x/2 rozwiązaniem; x = 2a/3, y = 2a/3 , G(2a/3,2a/3)
Odległości
OF
2 = (a/3 − 0)
2 + (a/3 − 0)
2 = 2*a
2/9 ⇒ OF = a*
√2/3
GF
2 = (2a/3 − a/3)
2 + (2a/3 − a/3)
2 = a
2/9 + a
2/9 = 2a
2/9 ⇒ GF = a
√2/3
GC
2 = (a − 2a/3)
2 + (a − 2a/3)
2 = a
2/9 + a
2/9 = 2a
2/9 ⇒ GC = a
√2/3
Wniosek: OF = FG = GC
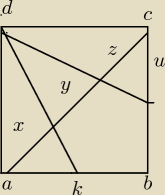 Proszę pomóżcie mam udowodnić że x=y=z.
U to jest połówka odcinka ab .Bardzo proszę o pomoc
Proszę pomóżcie mam udowodnić że x=y=z.
U to jest połówka odcinka ab .Bardzo proszę o pomoc
 Dowód metodą analityczną
Przyjąłem bok kwadratu OA = a. Wtedy
O(0,0) , A(a,0) , B(0,a) , C(a,a) , D(a/2,0) , E(a,a/2)
Równania prostych:
OC: y − 0 = (a − 0)/(a − 0)*(x − 0) ⇒ y = x
BD: y − a = (0 − a)/(a − a/2)*(x − a) ⇒ y = −2*x + a
BE: y − a = (0 − a/2)/(a − 0)*(x − 0) ⇒ y = a − x/2
Punkty przecięcia prostych
Punkt F − rozwiązuję układ równań
y = x
y = −2*x + a rozwiązaniem: x = a/3 , y = a/3 , F(a/3,a/3)
Punkt G rozwiązuję układ równań
y = x
y = a − x/2 rozwiązaniem; x = 2a/3, y = 2a/3 , G(2a/3,2a/3)
Odległości
OF2 = (a/3 − 0)2 + (a/3 − 0)2 = 2*a2/9 ⇒ OF = a*√2/3
GF2 = (2a/3 − a/3)2 + (2a/3 − a/3)2 = a2/9 + a2/9 = 2a2/9 ⇒ GF = a√2/3
GC2 = (a − 2a/3)2 + (a − 2a/3)2 = a2/9 + a2/9 = 2a2/9 ⇒ GC = a√2/3
Wniosek: OF = FG = GC
Dowód metodą analityczną
Przyjąłem bok kwadratu OA = a. Wtedy
O(0,0) , A(a,0) , B(0,a) , C(a,a) , D(a/2,0) , E(a,a/2)
Równania prostych:
OC: y − 0 = (a − 0)/(a − 0)*(x − 0) ⇒ y = x
BD: y − a = (0 − a)/(a − a/2)*(x − a) ⇒ y = −2*x + a
BE: y − a = (0 − a/2)/(a − 0)*(x − 0) ⇒ y = a − x/2
Punkty przecięcia prostych
Punkt F − rozwiązuję układ równań
y = x
y = −2*x + a rozwiązaniem: x = a/3 , y = a/3 , F(a/3,a/3)
Punkt G rozwiązuję układ równań
y = x
y = a − x/2 rozwiązaniem; x = 2a/3, y = 2a/3 , G(2a/3,2a/3)
Odległości
OF2 = (a/3 − 0)2 + (a/3 − 0)2 = 2*a2/9 ⇒ OF = a*√2/3
GF2 = (2a/3 − a/3)2 + (2a/3 − a/3)2 = a2/9 + a2/9 = 2a2/9 ⇒ GF = a√2/3
GC2 = (a − 2a/3)2 + (a − 2a/3)2 = a2/9 + a2/9 = 2a2/9 ⇒ GC = a√2/3
Wniosek: OF = FG = GC