Przekształcanie Wielomianów Łukasz : Rozwiąż równanie: 9x²=3x+2 Rozwiąż nierówność: 2x²+3x≥2 Czy ktoś może mi wytłumaczyć na powyższych przykładach, jak rozwiązuje się tego typu równania oraz nierówności wielomianowe. Z góry dziękuje

Kejt: 9x²=3x+2 9x²−3x−2=0 Δ=9+9*4*2=81 √Δ=9

	3−9
x1=		=...
	18

	3+9
x2=		=...
	18

Kejt: w drugim postępujesz bardzo podobnie, tylko z tą różnicą, że rozwiązaniem będzie przedział. Jak wyliczysz tam miejsca zerowe to Ci narysuję

Łukasz: 2x²+3x−2 Δ=9−4(2)(−2) Δ=25 √Δ=5 x₁=−2

	1
x2=
	2

x∊<−∞;−2)U<¹₂;+∞)

Łukasz: Kejt, chyba dobrze rozwiązałem,proszę o narysowanie tego wykresu i wytłumaczenie. Mam kolejne przykłady do rozwiązania ale nieco trudniejsze o to jeden z nich: x⁴−4x³+x−4>0 (x−√2)²(x−2)²(x+√3)≥0

Kejt:

	1
interesują nas wartości nieujemne, więc tak jak napisałeś..no prawie.. x∊(−∞;−2>u<		;+∞)
	2

Kejt: przy pierwszym najpierw pogrupuj ten wielomian i oblicz miejsca zerowe.

Łukasz: Pogrupować hmm? przed nawias nie można wyciągnąć więc jak mam go pogrupować?

Kejt: jak nie można? x⁴−4x³+x−4>0 x³(x−4)+1(x−4)>0 (x³+1)(x+4)>0 teraz policz miejsca zerowe

Łukasz: x∊(−∞;−1)u(4;+∞) Czyli wykres będzie wyglądał tak samo jak poprzednio?

Kejt: wynik jest ok, ale wykres nie będzie parabolą..

Łukasz: Nie wiem czy mi się wydaje, czy tam nie wkradł ci się błąd(x³+1)(x+4)>0 czy tu nie powinno być x−4

Kejt: ups..literówka..

Łukasz: A co to drugiego przykładu? pomożesz mi czy już nie masz siły

;): Z tym masz problem? (x − √2)²(x − 2)²(x + √3) ≥ 0

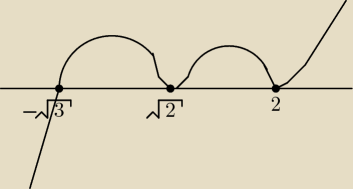
Kejt: wygląda to mniej więcej w ten sposób..

Łukasz: Czyli wystarczyło tylko nawiasy przyrównać do zera i i narysować wykres. Dzięki za pomoc Kejt