wykładnicza
Monika: Dobrze to zrobiłam?
−33x + 32x+1 + 3 * 3x+3 − 243 = 0
t = 3x, t>0
−t3 + 3t2 + 81t − 243 = 0
−t2(t − 3) +81(t − 3) = 0
(t − 3)(−t2 + 81) = 0
−(t −3)(t2 − 81) = 0
−(t − 3)(t − 9)(t + 9) = 0
1o
t = 3
3x = 31
x = 1
2o
t = 9
3x = 32
x = 2
3o
t = −9 ∉ t > 0
17 maj 12:42
Monika: Sprawdzi ktoś?
17 maj 12:53
;): W porządku

17 maj 12:55
Godzio:
Jest ok

17 maj 12:55
Monika: A coś takiego:?
43x − 2 * 42x+1 + 5 * 4x+1 − 16 = 0
t = 4x, t>0
t3 − 8t2 + 20t − 16 = 0
Dobrze do formy doprowadziłam?
17 maj 12:58
Godzio:
Tak

17 maj 12:58
Monika:
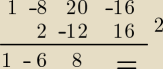
W(t) = t
3 − 8t
2 + 20t − 16
W(1) = 1 − 8 + 20 − 16 ≠ 0
W(−1) = −1 − 8 − 20 − 16 ≠ 0
W(2) = 8 − 32 + 40 − 16 = 0
Skoro jest podzielne przez dwa to:
(t − 2)(t
2 − 6t + 8) = 0
Δ = 36 − 32 = 4
(t−2)
2(t − 4) = 0
1
o
t = 2
4
x = 2
2
o
t = 4
4
x = 4
1
x = 1
17 maj 13:02
Monika: Logarytmów jeszcze nie miałam, więc 4x = 2 zostawić w takiej formie?
17 maj 13:03
Godzio:
4
? = 2

?
17 maj 13:03
;): t3 − 4t2 − 4t2 + 16t + 4t − 16 = 0
t2(t − 4) − 4t(t − 4) + 4(t − 4) = 0
(t − 4)(t2 − 4t + 4) = 0
(t − 4)(t − 2)2 = 0
17 maj 13:04
Godzio: Nie trzeba korzystać z logarytmów, żeby to rozwiązać
17 maj 13:04
Jack:
zapisz tak:
4x=2
22x=21
2x=1
x=1/2
17 maj 13:04
Jack:
ups...

Sorry
17 maj 13:04
Godzio:
No i jest gotowiec

17 maj 13:05
Monika: UPS

4
x = 2
2
2x = 2
1
2x = 1 / : 2
Ale z logarytmów można by skorzystać ?

17 maj 13:06
;): Heh
Jack 
17 maj 13:06
;): 4x = 412
17 maj 13:06
;): Można tylko że nie potrzebnie

log
42 = x
17 maj 13:08
Monika: A takie coś:
| | 1 | | 26 | |
3x * |
| − 3x * 3 = − |
| |
| | 9 | | 9 | |
i wyjdzie, że x = 0
Dobrze?
17 maj 13:09
Monika: To ostatnie zadanie:
5x+2 − 7 * 5x > 450
5x * 25 − 7 * 5x > 450
5x(25 − 7) > 450
5x * 18 > 450 : / 18
5x > 52
x>2
x∊(2, ∞)
17 maj 13:11
Monika: 
17 maj 13:42
Monika: ?
17 maj 14:01
Sabin: Oba ok
17 maj 14:13
Monika: A taka nierówność?
Sorki, że tak dużo tych nierówności ale dawno je miałam, koleżance obiecałam, że zrobię.
2
−x ≥ 2
6
−x≥ 6
x ≤ −6
x∊(−
∞,−6>
Istnieje jakiś inny sposób na to?
17 maj 14:39
Sabin:
Sposobów jest pewnie z 5, tylko po co je stosować, skoro tak jak zrobiłaś jest w zupełności ok?
17 maj 14:41
Monika: Przyszedł mi do głowy jeszcze jeden:
Ale czegoś mi tu brakuje, hmm
17 maj 14:43
Sabin:
| | 1 | |
Powinna być ( |
| ) do −6 po prawej. |
| | 2 | |
17 maj 14:45
Monika: Racja

17 maj 14:46
17 maj 14:46
Monika: Czy dla nierówności:
a = x
2 − 3
napisałam a dlatego że potęga potęgi nie działała

rozwiązanie to x∊(−
∞, − 3)U(1, +
∞)
| | 7 | |
to x∊(−∞, − |
| > dobre te rozwiązania? |
| | 3 | |
17 maj 15:31
Monika: 
17 maj 15:35
Sabin: ok!
17 maj 15:43
Monika: Dzięki!
17 maj 15:45



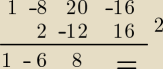 W(t) = t3 − 8t2 + 20t − 16
W(1) = 1 − 8 + 20 − 16 ≠ 0
W(−1) = −1 − 8 − 20 − 16 ≠ 0
W(2) = 8 − 32 + 40 − 16 = 0
Skoro jest podzielne przez dwa to:
(t − 2)(t2 − 6t + 8) = 0
Δ = 36 − 32 = 4
W(t) = t3 − 8t2 + 20t − 16
W(1) = 1 − 8 + 20 − 16 ≠ 0
W(−1) = −1 − 8 − 20 − 16 ≠ 0
W(2) = 8 − 32 + 40 − 16 = 0
Skoro jest podzielne przez dwa to:
(t − 2)(t2 − 6t + 8) = 0
Δ = 36 − 32 = 4
 ?
?
 Sorry
Sorry

 4x = 2
22x = 21
2x = 1 / : 2
4x = 2
22x = 21
2x = 1 / : 2


 log42 = x
log42 = x


 rozwiązanie to x∊(−∞, − 3)U(1, +∞)
rozwiązanie to x∊(−∞, − 3)U(1, +∞)
