. Kasia: Błagam o pomoc:( 1. W równolegloboku o obwodzie 40 cm przekątne sa dwusiecznymi kątów, a ich dlugosci maja sie do siebie jak 3:4. Oblicz dlugosci tych przekatnych 2. W trapezie rownoramiennym ABCD, AB II CD, wysokosc CE podzielila dluzsza podsatwe na odcinki majace dlugosc I AE I = 15 cm, I EB I = 6 cm. Długosc przekatnej DB jest rowna 17 cm. a) oblicz obwod tego trapezu b) jaka dlugosc ma odcinek laczacy srodki ramion tego trapezu? blagam o pomoc, nie umiem sobie z nimi poradzic.. function(searchElement){"use strict";if(this===void 0||this===null)throw new TypeError();var t=Object(this);var len=t.length>>>0;if(len===0)return-1;var n=0;if(arguments.length>0){n=Number(arguments[1]);if(n!==n)n=0;else if(n!==0&&n!==(1/0)&&n!==-(1/0))n=(n>0||-1)*Math.floor(Math.abs(n))}if(n>=len)return-1;var k=n>=0?n:Math.max(len-Math.abs(n),0);for(;k<len;k++){if(k in t&&t[k]===searchElement)return k}return-1}

Godzio: 1. Jaki równoległobok ma własność, że jego przekątne są dwusiecznymi kątów ?

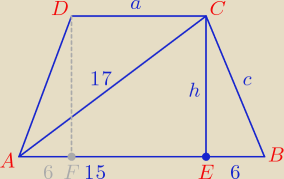
Godzio: |DB| = |AC| = 17 cm |AF| = |EB| = 6 cm 17² = 15² + h² ⇒ 289 = 225 + h² ⇒ h² = 64 ⇒ h = 8 h² + 6² = c² ⇒ 64 + 36 = c² ⇒ c² = 100 ⇒ c = 10 a = 15 − 6 = 9 L = 21 + 9 + 20 = 50 cm

	9 + 21
x =		= 15
	2

Kasia: hm, a nie każdy rownoleglobok ma taką własnosc? function(searchElement){"use strict";if(this===void 0||this===null)throw new TypeError();var t=Object(this);var len=t.length>>>0;if(len===0)return-1;var n=0;if(arguments.length>0){n=Number(arguments[1]);if(n!==n)n=0;else if(n!==0&&n!==(1/0)&&n!==-(1/0))n=(n>0||-1)*Math.floor(Math.abs(n))}if(n>=len)return-1;var k=n>=0?n:Math.max(len-Math.abs(n),0);for(;k<len;k++){if(k in t&&t[k]===searchElement)return k}return-1}

Kasia: przepraszam nie wiem co to jest co się dopisuje na koncu moich wiadomosci function(searchElement){"use strict";if(this===void 0||this===null)throw new TypeError();var t=Object(this);var len=t.length>>>0;if(len===0)return-1;var n=0;if(arguments.length>0){n=Number(arguments[1]);if(n!==n)n=0;else if(n!==0&&n!==(1/0)&&n!==-(1/0))n=(n>0||-1)*Math.floor(Math.abs(n))}if(n>=len)return-1;var k=n>=0?n:Math.max(len-Math.abs(n),0);for(;k<len;k++){if(k in t&&t[k]===searchElement)return k}return-1}

Godzio: Nie ma sprawy, pierwszego zadania Ci nie odpuszczę Nie każdy równoległobok ma taką własność, jaki dokładnie ? Pomyśl ...

Eta:

Kasia: pewnie równoramienny.. chociaż musze przyznać, że strzelam bo jakoś wydaje mi się, że w każdym tak jest, ale jak widać się myle.. eh, nie widze tego function(searchElement){"use strict";if(this===void 0||this===null)throw new TypeError();var t=Object(this);var len=t.length>>>0;if(len===0)return-1;var n=0;if(arguments.length>0){n=Number(arguments[1]);if(n!==n)n=0;else if(n!==0&&n!==(1/0)&&n!==-(1/0))n=(n>0||-1)*Math.floor(Math.abs(n))}if(n>=len)return-1;var k=n>=0?n:Math.max(len-Math.abs(n),0);for(;k<len;k++){if(k in t&&t[k]===searchElement)return k}return-1}

Godzio: No strzelasz strzelasz Nie ma "równoległoboku równoramiennego" Przeczytaj sobie o rombie

Kasia: maaatko, jakie ja głupoty pisze <dureń ze mnie> , nie wiem czemu ale pomylilam rownoleglobok z trapezem, nie bij! jeden jest równoległobok noo! function(searchElement){"use strict";if(this===void 0||this===null)throw new TypeError();var t=Object(this);var len=t.length>>>0;if(len===0)return-1;var n=0;if(arguments.length>0){n=Number(arguments[1]);if(n!==n)n=0;else if(n!==0&&n!==(1/0)&&n!==-(1/0))n=(n>0||-1)*Math.floor(Math.abs(n))}if(n>=len)return-1;var k=n>=0?n:Math.max(len-Math.abs(n),0);for(;k<len;k++){if(k in t&&t[k]===searchElement)return k}return-1}

Kasia: czyli jedno już wiem, że jest to romb dwa : bok każdy wynosi 10 cm function(searchElement){"use strict";if(this===void 0||this===null)throw new TypeError();var t=Object(this);var len=t.length>>>0;if(len===0)return-1;var n=0;if(arguments.length>0){n=Number(arguments[1]);if(n!==n)n=0;else if(n!==0&&n!==(1/0)&&n!==-(1/0))n=(n>0||-1)*Math.floor(Math.abs(n))}if(n>=len)return-1;var k=n>=0?n:Math.max(len-Math.abs(n),0);for(;k<len;k++){if(k in t&&t[k]===searchElement)return k}return-1}

Godzio: Przekątne przecinają się pod kątem ... ?

Kasia: prostyyym czyli licze po prostu je z twierdzenia Pitagorasa, a później układam tak jakby proporcje tzn przekatna 1 / przekatna 2 = 3/4 , tak? function(searchElement){"use strict";if(this===void 0||this===null)throw new TypeError();var t=Object(this);var len=t.length>>>0;if(len===0)return-1;var n=0;if(arguments.length>0){n=Number(arguments[1]);if(n!==n)n=0;else if(n!==0&&n!==(1/0)&&n!==-(1/0))n=(n>0||-1)*Math.floor(Math.abs(n))}if(n>=len)return-1;var k=n>=0?n:Math.max(len-Math.abs(n),0);for(;k<len;k++){if(k in t&&t[k]===searchElement)return k}return-1}

Godzio: Ok Wiedząc że przekątna są w stosunku 3 : 4, to dla ułatwienia można ich połówki oznaczyć 3x i 4x Więc jedynie co masz do rozwiązania: (3x)² + (4x)² = 10² ⇒ x = ... Przekątna mają długość 8x i 6x

Kasia: ok, rozumiem Dzięki wielkie! No, takiego nauczyciela bym mogła mieć, od razu jasne wszystko function(searchElement){"use strict";if(this===void 0||this===null)throw new TypeError();var t=Object(this);var len=t.length>>>0;if(len===0)return-1;var n=0;if(arguments.length>0){n=Number(arguments[1]);if(n!==n)n=0;else if(n!==0&&n!==(1/0)&&n!==-(1/0))n=(n>0||-1)*Math.floor(Math.abs(n))}if(n>=len)return-1;var k=n>=0?n:Math.max(len-Math.abs(n),0);for(;k<len;k++){if(k in t&&t[k]===searchElement)return k}return-1}

Godzio:

Eta: Widzisz Godzio ...... musisz koniecznie zostać nauczycielem

Godzio: Chciałbym ...

Eta: Witam w "gronie"

Godzio: