wykaż, że
Monika:
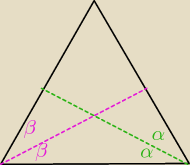
Udowodnij, że w trójkącie równoramiennym dwusieczne kątów przy podstawie są równej długości.
Jak to zrobić na podstawie przystawania trójkątów?
16 maj 21:49
adrian:
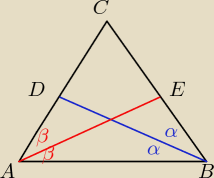
2α = 2β
α = β
AEB przystaje do ABD
no i chyba dalej wiadomo
16 maj 21:55
Monika: Możesz całość napisać?
16 maj 21:56
;):
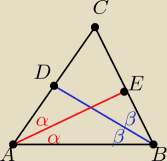
α = β
ΔABD ~ ΔABE (kkk)
16 maj 22:12
Monika: Mi mówili że z kąt−bok−kąt
16 maj 22:17
Monika: | | |AE| | | |AB| | |
i nie powinna być proporcja: |
| = |
| ? Mnie w szkole uczyli, |
| | |BD| | | |AB| | |
16 maj 22:20
Monika: Pomocy
16 maj 22:32
Monika: Pomocy
17 maj 12:22
voltage: | |AE| | | |AB| | | |AE| | | |BD| | |
| = |
| jest proporcją równoważną do |
| = |
| , więc |
| |BD| | | |AB| | | |AB| | | |AB| | |
wszystko się zgadza
17 maj 12:28
Monika: I to będzie |AE| = |BD| czyli kbk?
17 maj 12:29
voltage: Będzie i kbk i kkk
17 maj 12:31
Monika: czemu kkk?
17 maj 12:31
voltage: Też jest bbb, ale masz rację, że żeby udowodnij przystawanie tych trójkątów to trzeba uzasadnić
to cecha kbk
17 maj 12:32
Monika:
17 maj 12:33
voltage: Zauważ że jeśli α=β to każdy z tych trójkątów ma kąty 2α,α i jakiś tam kąt (np.γ) czyli jest
tez kkk. Jednak cechą kkk można uzasadnić podobieństwo, a nie przystawanie dlatego uzasadniasz
to kbk.
17 maj 12:36
Monika: Ale kbk też może być
17 maj 12:38
gupiaty: Nie ma cechy kkk. Przecież wszzystkie trojkaty rownoboczne maja w kazdym kacie po 60 stopni,
jednak ich wielkosc moze byc rowna i niekoniecznie znaczy to ze sa przystajace
13 sty 17:30