Kupa zadań ale prostych fdghhh: tu http://www.scribd.com/fullscreen/55558945?access_key=key-czfhacid9sc87ieu7qx i tu http://www.scribd.com/fullscreen/55558612?access_key=key-1kixh389hmeuvjnrf00o Proszę o rozwiązania a nie same odpowiedzi.Dlaczego sam nie zrobie?mam zaliczenie z innego przedmiotu i dam rady samemu.

podpis.: zad1. 6% −−−−−> 9 100% −−−−− x mnożymy na ukos 6x = 900 x = 150 zad2. na osi widzisz przedział jeden to znaczy nie takie coś jak u mnie na rysunku, że z obu stron tylko jeden. czyli będzie to A, C lub D bo one mają "≤" wyznaczasz sobie środek przedziału {6+2}{2} = −2 i teraz już wiesz x = −2 czyli x + 2 = 0 odpC. |x+2| ≤ 4

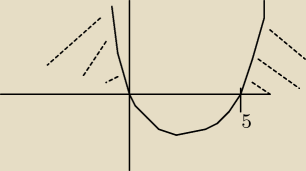
podpis.: |x+2| ≤ 4 <−−−−−− ten zapis oznacza że odległość od −2 jest mniejsza bądź równa 4 i sprawdź czy to się zgadza. napewno. zad3. zbiór wartości to znaczy jakie przyjmuje y−ki y∊<−2,5> odp B A nie może być bo tam jest przedział otwarty, a ponieważ −2 i 5 też należy do zbioru wartości więc y∊<−2,5> odp B zad4.odp D ja sobie podstawiałem. jak dałem m=3 to wzór funkcji=2x+2 no i to nie zgadza się z założeniem, że dodatnie jest tylko dla x<1 bo dla x=5 bedzie 12 jak podstawiłem x=1 to funkcji wygląda tak: y=2 czyli jest stała (zawsze dodatnia). jak podstawiłem x=0 to y = −x + 2 i zauważ ze to jest dadatnie także dla x=1, czyli nie spełnia założenia i ostatnie y= −2x + 2 widać ze dla x=1 funkcji jest równa zero czyli dopiero dla x<0 jest dodatnia. zad5. 3(1− x) + x > 3(3−2x) wymnażam to 3 −3x + x > 9 − 6x 3 −2x > 9 − 6x 4x > 6 x> ⁶₄ x > ³₂ Odp.: D bo tylko √5 jest >³₂. zad6. podstawiamy za x wartości miejsc zerowych, czyli: 0 = a(−2)² + 3*(−2) − 6 0 = a*1 + 3*1 − 6 0 = 4a −6 −6 0 = a + 3 − 6 0 = 4a − 12 0 = a − 3 a = 3, Odp.:a. zad7. układ równań a− długość krutszego boku, b−długość dłuższego boku. ab=12 2a+2b=14 ab = 12 a + b = 7 ab = 12 a = 7 − b (7−b)b = 12 a = 7−b 7b − b² − 12 = 0 a = 7 − b −b² + 7b − 12 = 0 a = 7 − b pamiętajmy zawsze że a i b >0 (bo to sa długości boków i nie mogą być < 0) −b² + 7b − 12 = 0 Δ = 49 − 48 = 1 √Δ = 1 b₁ = ⁻⁷⁻¹₋₂ = 4 b₂ = ⁻⁷⁺¹₋₂ = 3 czyli a₁ = 3 a₂ = 4 widzimy, że albo mamy pare 3 i 4 albo 4i 3 czyle ze to to samo Odp C przekątna ma długość 5, można to łatwo obliczyć z twierdzania pitagorasa, oznaczmy przekątna przez p p² = a² + b² = 9+16 = 25 x = √25 = 5 zad8. x² > 5x x² − 5x > 0 x (x − 5) > 0 x=0 (lub)∨ x=5 ramiona skierowane w górę i jest to parabola większe od zera (tam gdzie przerywane linie) dla x∊ (−∞, 0) ∪ (5, +∞) Odp.::B zad9. jedynka trygonometryczna sin²α + cos²α = 1 cos = √1 − sin²α = √1−¹⁶₂₅ = √⁹₂₅ = ³₅ Odp.:A drugą ture spróbuj zrobić sam jak nie będziesz umiał to napisz, ale próbuj.