help
ikson : pomóżcie !
Przekatne trapezu dzielą go na cztery trójkąty. Oblicz pole trapezu, wiedzac, że pola trójkątów
przyległych do podstaw trapezu są równe 16 i 9.
Prosze o dokładne rozpisanie
oraz z góry dziękuję !
Bogdan:
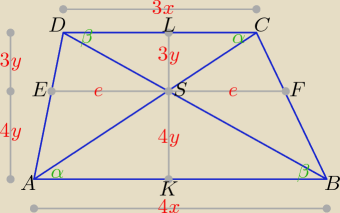
Trójkąty ABS i CDS są podobne w skali k.
I sposób
| PABS | | 16 | | 4 | |
| = |
| = k2 ⇒ k = |
| |
| PCDS | | 9 | | 3 | |
| |AB| | | 4 | | 1 | |
| = |
| , |AB| = 4x, |CD| = 3x, |
| *4x*4y = 16 ⇒ xy = 2 |
| |CD| | | 3 | | 2 | |
| |KS| | | 4 | |
| = |
| , |KS| = 4y, |LS| = 3y |
| |LS| | | 3 | |
Korzystam z wzoru na długość odcinka EF łączącego ramiona trapezu, równoległego do jego
podstaw i przechodzącego przez punkt przecięcia przekątnych oraz z równości odcinków
| | |AB| * |CD| | | 12x2 | | 12 | |
ES i FS: |ES| = |FS| = e = |
| = |
| = |
| x |
| | |AB| + |CD| | | 7x | | 7 | |
| | 1 | | 1 | | 1 | | 12 | |
PASD = PBSD = |
| *e*4y + |
| *e*3y = |
| * |
| x*7y = 6xy = 6*2 = 12 |
| | 2 | | 2 | | 2 | | 7 | |
Pole trapezu P
ABCD = P{ABS} + P
CDS + P
BCS + P
ASD = 16 + 9 + 12 + 12 = 49
II sposób
Korzystam z wzoru na pole trapezu P
ABCD = (
√PABS +
√PCDS )
2
W tym zadaniu P
ABCD = (
√16 +
√9)
2 = 7
2 = 49
Przy okazji − pola trójkątów BCS i ASD wyrażają się wzorem:
P
BCS = P
ASD =
√PABC*PCDS