matematykaszkolna.pl
Trójkąty. Sylwia:
 x y 
Niech P będzie dowolnym punktem wewnętrznym trójkąta ABC. Wykaż, że
+
+
 h1 h2 
 z 
= 1, gdzie x, y, z oznaczają odległości tego punktu od boków trójkąta, a h1, jh2,
 h3 
h3 są długościami wysokości poprowadzonych odpowiednio na te boki.
16 maj 18:55
Sylwia: Podbijam
16 maj 19:05
Eta: Pomogę, cierpliwości, rysuję
16 maj 19:15
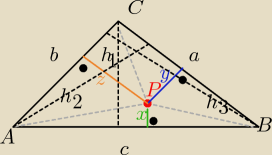Eta: rysunek P(ΔABC) = P(ΔAPB) + P(ΔBPC) + P(ΔAPC)
 c*x a*y b*z 
P=
+
+
| : P
 2 2 2 
 c*x a*y b*z 
1=
+
+
 2P 2P 2P 
c*x a*y b*z 
+
+
=1
h1*c a*h2 b*h3 
 x y z 
+
+
= 1
 h1 h2 h3 
c. n. u. emotka
16 maj 19:29
Sylwia: Dziękuję emotka
16 maj 19:57