Planimetria voltage: Witam! Wewnątrz trójkąta ABC znajduje się punkt P. Przez ten punkt przechodzą trzy proste równoległe do boków trójkąta, dzieląc go na trzy trójkąty i trzy równoległoboki. Udowodnij że √S=√S₁ +√S₂ +√S₃, gdzie S− pole trójkąta ABC, S₁, S₂, S₃− pola trójkątów otrzymanych. Proszę o pomoc.

voltage: Raise!

voltage: Raise

voltage: UP

Anusia17: cześć Czy możesz mi pomóc z tymi zadaniami? Z góry dziękuję Zadanie 1 Mając dane zbiory : A = <3, 6) i B = (4,8) oblicz: . Zadanie 2 Oblicz: a) 13,7+(−2,6):0,5+(−1,5).6= b) Zadanie 3 Przedstaw w postaci potęgi liczby 2: (2−4: 2−2) : (2−5: 2−4)= Zadanie 4 Doprowadź do prostszej postaci wyrażenia: . Zadanie 5 Oblicz wartość liczbową wyrażenia : (x + 2y)(x − 2y) – 4x(x − y)+ (x − 2y)2− y dla x = 0,5 i y= − 0,5 Zadanie 6 Cenę pewnego towaru podwyższono najpierw o 20%, a potem jeszcze o 10%. Oblicz rzeczywista podwyżka w procentach. Zadanie 7 Oblicz: log 5 + log 8 – 2 log 2. Zadanie 8 W trapezie równoramiennym ABCD podstawy mają długość 10cm i 4cm, a ramię BC ma długość 6cm. Oblicz wysokość i obwód tego trapezu.

voltage: Dlaczego nie napisałaś w osobnym poście? Poza tym większość z tych zadań jest zapisana w taki sposób, że nie wiadomo o co chodzi.

voltage: UP

voltage: UP

Jack: zauważ, że w w trójkącie znajdziesz trzy inne podobne trójkąty (sumie trzy małe i jeden duży). Potem korzystaj kilka razy z podobieństwa dla pól... Zauważ, że podstawy trzech małych trójkątów tworzą podstawę dużego trójkąta... powinno łatwo wyjść Nie chcę Ci psuć zabawy

voltage: Dzięki

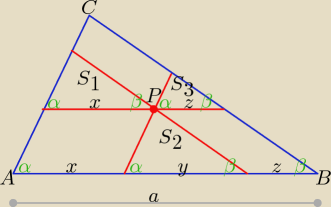Bogdan: Myślę Jack, że warto pokazać rozwiązanie tego bardzo sędziwego zadania. Jest ono publikowane od wielu dziesiątek lat, a kilka lat temu pojawiło się podczas matury. a = x + y + z Trójkąty o polach S₁, S₂, S₃ i trójkąt ABC o polu S są podobne.

x		√S1		y		√S2		z		√S3
	=		,		=		,		=		,
a		√S		a		√S		a		√S

	√S1		√S2		√S3
x = a*		, y = a*		, z = a*
	√S		√S		√S

	√S1		√S2		√S3		√S
a = a*		+ a*		+ a*		/ *		,
	√S		√S		√S		a

√S = √S₁ + √S₂ + √S₃, co należało udowodnić.

Jack: to prawda, stare zadanie. Kiedyś znalazłem je w zbiorze Inglota. Bardzo ciekawe zadanie, dlatego tym bardziej chciałem zostawić je dla voltage. Faktycznie, rozwiązanie na forum może się okazać przydatne dla innych osób.

voltage: Hehe jak to wczoraj robiłem to rozpisałem te wzory na pole trójkąta jeszcze i zajęło mi to co najmniej 2x tyle, ale później i tak się skróciło