Zadanie z rombem Ruda: Bok rombu ma długość 4 cm, a suma długości jego przekątnych jest równa 10 cm. Oblicz pole i wysokość tego rombu.

ICSP: e,f przekątne e + f = 10

	e		f
(		)2 + (		)2 = 16.
	2		2

Ruda: Dalej nic z tego nie wynika....

ICSP:

	e*f
jak wylicz e i f możesz policzyć pole rombu z tego wzorku: P =		. Później mająć pole
	2

	P
rombu liczysz jego wysokość: P = ah ⇔ h =
	a

Ruda: ^e2₄ + ^f2₄ = 16 I jak mam z tego wyliczyć ? ^e2₄ = 16 − ^f2₄

ICSP: po pierwsze przemnóż przez 4: e² + f² = 64 pierwsze równanie : e + f = 10 f = 10 − e teraz podstawiając do drogiego równania

	10 + √28		10−√28
e2 + (10−e)2 = 64 ⇔ e2 −10e + 18 = 0 ⇔ e1 =		oraz e2 =
	2		2

weźmiemy e₁ to wtedy f możemy zapisać jako e₂ dlatego:

	10 + √28		10−√28
e =		⇔ f =		(lub na odwrót)
	2		2

Ruda: ja pierdziele... Dzięki

Bogdan:

	1
P =		*2x*2y ⇒ P = 2xy
	2

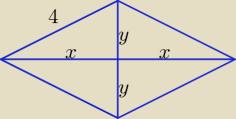
x² + y² = 16 2x + 2y = 10 ⇒ x + y = 5 /² ⇒ x² + 2xy + y² = 25 ⇒ 16 + P = 25 ⇒ P = 9 P = a*h ⇒ 9 = 4h ⇒ h = ...

Ruda: Dziękuje, że ktoś to napisał po polsku