bardzo proszę o pomoc michał: Bardzo proszę Was o pomoc. Chociaż proszę o radę jak to zacząć Oblicz pole ośmiokąta wpisanego w okrąg oraz promień okręgu,w którym cztery kolejne boki mają długość 3, a cztery pozostałe boki mają długość 2.

michał: Mógłby ktoś pomóc?

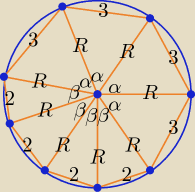
Bogdan: 4α + 4β = 360^o ⇒ α + β = 90^o ⇒ β = 90^o − α ⇒ sinβ = cosα Z twierdzenia sinusów:

3		3
	= 2R ⇒ sinα =
sinα		2R

2		1
	= 2R ⇒ sinβ = cosα =
sinβ		R

sin²α + cos²α = 1 ⇒ ...., stąd wyznacz R, potem oblicz sinα i sinβ.

	1		1
Pole tego ośmiokata P = 4*		R2sinα + 4*		R2sinβ
	2		2

michał: Wielkie dzięki