Dowody
Monika:
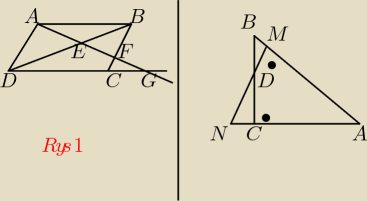
Mam następujące pytanie: dla zadania np.:
Prosta przechodząca przez wierzchołek A równoległoboku ABCD przecina jego przekątną BD
w punkcie E i bok BC w punkcie F, a prostą DC w punkcie G.
Udowodnij, żę |EA|
2 = |EF| * |EG| − rysunek pierwszy
Mamy proporcję taką:
Trójkąty AEB i DEG są podobne (cecha kkk):
A dla zadania:
Przez środek D przyprostokątnej BC trójkąta prostokątnego ABC poprowadzono prostą prostopadłą
do przeciwprostokątnej AB . Prosta ta przecina proste AB i AC odpowiednio w punktach M i N .
Wykaż, że |BC|
2 = 4 ⋅|DN |⋅|DM | .
I tutaj proporcja taka:
Pytanie: dlaczego ta druga proporcja jest inna?
a nie mogłoby być np.:
?
14 maj 21:55
Monika: Jakiś pomysł?
14 maj 22:05
14 maj 22:12
Monika: Ale ja nie pytam się jak to zrobić tylko czemu nie może być taka proporcja w drugim zadaniu

14 maj 22:13
Monika: Halo
14 maj 22:17
Godzio:
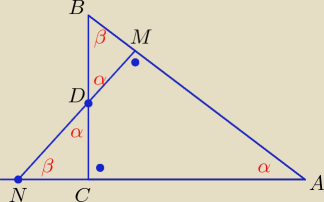
Z podobieństwa CND ~ BDM mamy:
|BD| * |DC| = |MD| * |DN|
|BC|
2 = 4 * |MD| * |DN|
c.n.d.
14 maj 22:18
Godzio:
A to sorki, pospieszyłem się, a dlaczego nie może być? Ano dlatego że takie proporcje nie
zachodzą, ustaw sobie te 2 trójkąty w tej samej pozycji, Ty zrobiłaś taką proporcję:
| DM | | DN | |
| = |
| −−− Taka proporcja nie zachodzi, bo DN jest przeciwprostokątną, a DM |
| DB | | CD | |
przyprostokątną
14 maj 22:22
Monika: Już rozumiem, dziękuje
14 maj 22:23
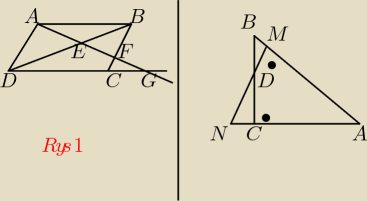 Mam następujące pytanie: dla zadania np.:
Prosta przechodząca przez wierzchołek A równoległoboku ABCD przecina jego przekątną BD
w punkcie E i bok BC w punkcie F, a prostą DC w punkcie G.
Udowodnij, żę |EA|2 = |EF| * |EG| − rysunek pierwszy
Mamy proporcję taką:
Trójkąty AEB i DEG są podobne (cecha kkk):
Mam następujące pytanie: dla zadania np.:
Prosta przechodząca przez wierzchołek A równoległoboku ABCD przecina jego przekątną BD
w punkcie E i bok BC w punkcie F, a prostą DC w punkcie G.
Udowodnij, żę |EA|2 = |EF| * |EG| − rysunek pierwszy
Mamy proporcję taką:
Trójkąty AEB i DEG są podobne (cecha kkk):

