Geometria
Matma: W romb o boku długości 4 i kącie ostrym 60 wpisano okrąg.Oblicz pole czworokąta ,którego
wierzchołki są punktami styczności okręgu z bokami rombu.
Ma ktoś pomysł jak to zrobić.
13 maj 21:00
ceaser I:
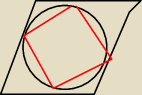
13 maj 21:58
ceaser I: z tw . cosinusów mozesz obliczyc boki czerwonej figury, bo punkt stycznośći dzieli bok na pół
13 maj 21:59
Eta:
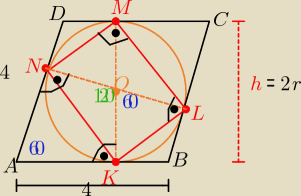
Czworokąt KLMN jest prostokątem, bo kąty NML , NKL, KNM , MLK
są wpisane i oparte na średnicy za tem są kątami prostymi
długość przekątnych jest d= 2r
katy między przekątnymi mają miary 120
o i 60
o
bo suma kątów w czworokącie AKON jest 360
o
| | 1 | |
zatem pole prostokąta jest: |
| d2*sin 600
|
| | 2 | |
wyzanaczamy długość 2r=h
| | h | |
|
| = sin60o => h=2r= 2√3
|
| | 4 | |
i liczymy teraz pole czworokata KLMN
| | 1 | | √3 | |
P= |
| *2√3*2√3*sin60o = √3*2√3* |
| = 3√3 [j2]
|
| | 2 | | 2 | |
13 maj 23:50
bart: @ceaser I
tak jest tylko w kwadracie

14 maj 00:30
ceaser I: 2x z cos 60 i 2x z cos 120
14 maj 11:13

 Czworokąt KLMN jest prostokątem, bo kąty NML , NKL, KNM , MLK
są wpisane i oparte na średnicy za tem są kątami prostymi
długość przekątnych jest d= 2r
katy między przekątnymi mają miary 120o i 60o
bo suma kątów w czworokącie AKON jest 360o
Czworokąt KLMN jest prostokątem, bo kąty NML , NKL, KNM , MLK
są wpisane i oparte na średnicy za tem są kątami prostymi
długość przekątnych jest d= 2r
katy między przekątnymi mają miary 120o i 60o
bo suma kątów w czworokącie AKON jest 360o
