pomoc onka: Blagam o wyjaśnienie rozwiązania bo nic nie rozumiem O zdarzeniach A B C Ω wiadomo że P(A)=¼ , P(B)=⅓ , P (AпB)=⅕. Oblicz: P(A' п B' ) i P(A' /B )

TOmek:

	1		3
P(A)=		P(A')=
	4		4

	1		2
P(B)=		P(B')=
	3		3

	1
P(AnB)=
	5

P(AuB)=P(A)+P(B)−P(AnB)

	1		1		1		7		1		35		12
P(AuB)=		+		−		=		−		=		−
	4		3		5		12		5		60		60

P(A'uB')=P(A')+P(B')−P(A' п B' )

TOmek: P(AuB)=1−P(A'uB') wynik P(A'uB') podstawiasz do wzoru P(A'uB')=P(A')+P(B')−P(A' п B' ) i otrzymujesz P(A' п B' )

TOmek: 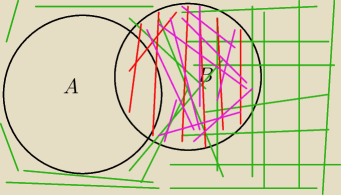zielone to P(A') czerwone P(B) P(A' /B ) czyli od cześci zielonej "wywalamy" czesc rózową

	3
Pierw obliczmy rozlowy kawałek: jest to P(B) − P(AnB)=1/2 − 1/5=
	10

	3		3
P(A' /B )=		−		= ........
	4		10

TOmek: myśle ,ze sie nie pomyliłem, sprawdź wyniki, jak sie zgadzaja i czegos nie wiesz to pytaj

TOmek: tam mam błąd P(A'uB')=1−P(AuB)=...