help aśka: 1. mamy dany układ równań i nierówności x²−4x−y+1≤0 y=1 dla x,y ∊ R . Jeśli długość boku kwadratu jest równa długości odcinka będącego rozwiązaniem tego układu równań i nierówności to ile wynosi pole i obwód tego kwadratu. 2. ile wynosi obwód i pole figury będącej rozwiązaniem układu równań i nierówności (x−3)²+(y−1)²=10 x−3y≤0

think: ad. 1. x² − 4x − y + 1 ≤ 0 y = 1 x² − 4x − 1 + 1 ≤ 0 ← to jest nierówność kwadratowa przez rozwiązanie, rozumie się przedział [x₁;x₂] długość tego przedziału x₂ − x₁ będzie długością boku kwadratu. Pole to (x₂ − x₁)² a obwód to 4*(x₂ − x₁)

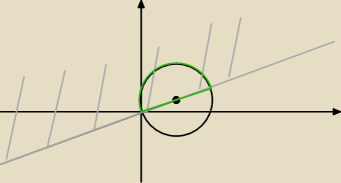
think: no tak się jakoś złożyło że część wspólna okręgu i tej półpłaszczyzny to połowa okręgu (zaznaczone na zielono). Obliczenie pola nie powinno być niczym trudnym, obwód też nie jest powalający