.
seba: funkcja f(m) przyporządkowuje liczbie rzeczywistej: m liczbę pierwiastków równania:
|3x2+2x−1|=m
naszkicój wykres tej funkcji.
12 maj 22:03
Anna: Pomogę i naszkic
uję.
12 maj 22:10
seba: jak miło
12 maj 22:15
Anna:
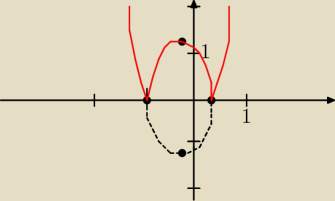
y = I3x
2+2x−1I
| | 1 | |
Δ=16, x1 = |
| , x2 = −1 (miejsca zerowe na wykresie) |
| | 3 | |
| | −b | | −1 | |
współrzędne wierzchołka: p= |
| = |
| |
| | 2a | | 3 | |
| | −Δ | | −16 | | −4 | |
q = |
| = |
| = |
| |
| | 4a | | 12 | | 3 | |
Zatem, na podstawie czerwonego wykresu, równanie ma:
0 pierwiastków dla m∊ (−
∞,0)
| | 4 | |
2 pierwiastki dla m=0 oraz m∊( |
| ,∞) |
| | 3 | |
| | 4 | |
3 pierwiastki dla m = |
| |
| | 3 | |
| | 4 | |
4 pierwiastki dla m ∊(0, |
| ). |
| | 3 | |
12 maj 22:32
seba: dziękuję fajnej pani za pomoc
12 maj 22:35
seba: będę wdzięczny jeżeli pomożesz mi jeszcze z tym:
dla jakich wartości parametru m równianie: x2+2(m+4)x+m2−2m=0
ma 2 różne pierwiastki rzeczywiste jednakowych znaków?
12 maj 22:38
Anna: Moment. Zaraz napiszę.
12 maj 22:46
seba: ok
12 maj 22:46
Anna:
Warunki: 1
0 . Δ>0 ⇔ b
2−4ac >0
[2(m+4)]
2 − 4(m
2−2m) > 0
4(m
2+8m+16) − 4m
2+8m >0 /:4
m
2+8m+16−m
2+2m >0
10m > −16 ⇒ m> −1,6
m
2 − 2m > 0
m(m−2) > 0
m=0, m=2
Na podstawie wykresu paraboli mamy: m∊ (−
∞,0) U (2,
∞).
Po połączeniu obu warunków (część wspólna) otrzymujemy odp.:
m∊( −1,6; 0) U(2,
∞).
12 maj 23:01
seba: 
12 maj 23:11