Trójkąt ABC Piotrek: w trójkącie abc bok ab ma długość a, natomiast bok BC ma długość b. Pole tego trójkąta P= ²₅ ab. Oblicz długość boku BC . Cały czas krążę wokół takich wzorów ²₅ab=¹₂ah b=⁵₄h I nie wiem, czy na tym może zostać, czy mam krążyć dalej.

Piotrek:

Piotrek:

Piotrek: Proszę o pomoc

Piotrek: Nie obliczyć, bok BC, tylko AC!

PanCogito: Ja bym próbował ze wzoru Herona

Piotrek: A nie ma jakiegoś prostszego sposobu, albo mógłby mnie ktoś naprowadzić na ten? No bo mam ten wzór i co dalej, przecież tego to się nawet wymnożyć nie da w momencie jak nie mam konkretnych liczb....

bart: zrobie

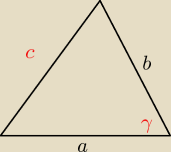
bart: Dane mamz a i b

	1
P=		sinγab i przyrownujemy
	2

1		2
	sinγab=		ab
2		5

	4
sinγ=
	5

1=sin²γ+cos²γ

	16
cos2γ=1−		γ−kat ostry wiec cosγ∊(0,1)
	25

	3
cosγ=
	5

z twierdzenia cosinusow mamy: c²=a²+b²−2abcosγ

	3
c2=a2+b2−2ab
	5

c=√....

Piotrek: Dziękuję

Piotrek: a może by mi tak ktoś mógł powiedzieć o co chodzi od 4 linijki tzn. dlaczego jest 1=.....

TOmek: jedynka trygonometryczna https://matematykaszkolna.pl/strona/450.html

Piotrek: aha Dziękuję

Piotrek: a jeszcze skąd wiemy, że jak wyszło 16/25 to jest kąt ostry