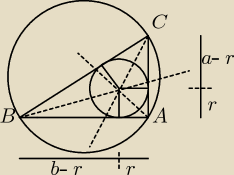 W trójkącie prostokątnym ABC przeciwprostokątna BC ma długość 13. Stosunek promienia koła
wpisanego w ten trójkąt do pla koła opisanego na tym trójkącie wynosi 413. Oblicz
tangensy kątów ostrych tego trójkąta.
Zacząłem rozwiązanie ale utknąłem:
AC=a
AB=b
BC=c=2*R − średnica koła opisanego na trójkącie
r − promień koła wpisanego w trójkąt
2*R=13
rπ*R2=413
stąd:r=13π
c=(b−r)+(a−r) −> c=b+a−2r −> b+a=c+2r
r=2Pa+b+c
P= r(c+r) ...... czy tędy droga? Jeśli tak to co dalej? Proszę o pomoc
W trójkącie prostokątnym ABC przeciwprostokątna BC ma długość 13. Stosunek promienia koła
wpisanego w ten trójkąt do pla koła opisanego na tym trójkącie wynosi 413. Oblicz
tangensy kątów ostrych tego trójkąta.
Zacząłem rozwiązanie ale utknąłem:
AC=a
AB=b
BC=c=2*R − średnica koła opisanego na trójkącie
r − promień koła wpisanego w trójkąt
2*R=13
rπ*R2=413
stąd:r=13π
c=(b−r)+(a−r) −> c=b+a−2r −> b+a=c+2r
r=2Pa+b+c
P= r(c+r) ...... czy tędy droga? Jeśli tak to co dalej? Proszę o pomoc
| r2π | 4 | |||
tam jest | = |  | ||
| R2π | 13 |