długości boków trójkąta anka: Długości boków pewnego trójkąta o obwodzie 60 pozostają w stosunku 5 :12 :13. Długość najkrótszej wysokości tego trójkąta jest równa... 120/13. Dlaczego taki wynik?

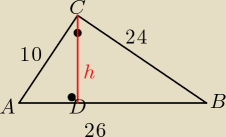
Eta: |AC|= 5x , |BC|= 12x , |AB| = 13x , x>0 5x +12x +13x= 60 => 30x= 60 => x=2 |AC| = 2*5=10 , |BC| = 12*2= 24 , | AB|= 13*2 = 26 Δ ABC jest prostokątny, bo : 26²= 10²+24²

	10*24
P(Δ ABC) =		= 120
	2

	|AB|*h
i P( Δ ABC) =
	2

	26*h
		= 120
	2

13h =120

	120
to: h=
	13

Gustlik: Eta − Ty masz dokładnie te same metody, co ja, prosto i przejrzyście. Pozdrawiam