planimetria kropka: Trójkąt ABC wpisano w okrąg. Poprowadzono wysokość z wierzchołka C i przedłużono ją do przecięcia z okręgiem w punkcie D. Wykaż, że I∡ADBI=I∡ASBI, gdzie S jest punktem przecięcia wysokości trójkąta ABC.

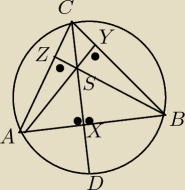
Vax: Zauważmy, że ∠CDA = ∠CBA oraz ∠CDB = ∠CAB, mamy więc dowieść, że ∠BAC + ∠CBA = ∠ASB, zauważmy, że na czworokącie AXSZ można opisać okrąg, więc ∠BAC = 180−∠ZSX = ∠XSB, podobnie ∠CBA = 180−∠YSX = ∠ASX, więc istotnie ∠BAC + ∠CBA = ∠XSB + ∠ASX = ∠ASB cnd.