Styczna Łukasz: Znajdź takie równanie takiej stycznej do wykresu funkcji f, która jest równoległa do prostej o podanym równaniu.

	1
f(x)=−		x2− 3x, y=x+11
	2

Proszę o pomoc, oto jedno z zadań na kartkówkę ze stycznej. Proszę o jego wykonanie wraz z dokładną analizą jak co się robi. Nie odsyłajcie mnie na wzory, bo już je widziałem i dalej nie mogę ogarnąć

Łukasz:

Łukasz: nikt nie umie

Łukasz: a ja nadal nie wiem

;): y = x + 11 prosta równoległa ma równanie y = x + b

	1
x + b = −		x2 − 3x / * 2
	2

x² + 8x + 2b = 0 Δ = 0 Δ = 16 − 2b 8 − b = 0 b = 8 Więc styczna ma postać g(x) = x + 8

Łukasz: dzięki

roman: a czy tam czasmi nie powinno byc prosta równoległa ma równanie y = ax+b

roman: bo zaraz rónoległa a₁=a₁

	1
a prostopadła =−
	a

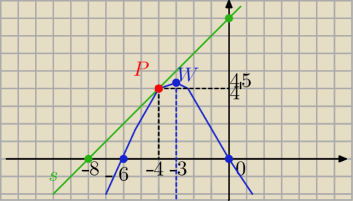
Eta: styczna ma równanie: s : y= x +b rozwiazujesz układ równań y= x+b

	1
y= −		x2 −3x ......... i nakładamy warunek na deltę : Δ= 0
	2

	1
−		x2−3x = x +b
	2

	1
−		x2 −4x −b=0
	2

Δ= 16 −2b => 16 −2b=0 => b= 8 to: s : y= x +8 co widać na załączonym rysunku , gdzie P −−− punkt styczności

roman: Da. dzięki za wytłumaczenie

??: może mi ktos powiedzieć skąd się wzięło 16 −2b

??:

	1
bo rozumiem że −		x2−4x−b=0 /*2 tak
	2

??: liczyłeś to ze zwykłego wzoru na deltę

Łukasz: Witajcie. Wszystko bardzo dobrze wyszło ale czy da się to wyliczyć wzorami na pochodną. y=x+b A(x₀,f(x₀) f'(x)=x−3 f'(x₀)=x₀−3 a=f'(x₀) 1=−x₀−3 −4=x₀ x₀=−4

	1
f(x0)=f(−4)=		(−4)2−3(−4)
	2

	16
f(x0)=		+12
	2

Nie wiem czy dobrze myślę, jeśli tak co trzeba dalej zrobić?

Łukasz: Pomożecie plx

Łukasz: Rzućcie okiem

Łukasz: hmm? nadal nic

Łukasz: Nadal odświeżam, zobaczcie czy dobrze robię. Pozdro