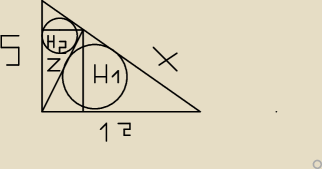Przez wierzchołek kąta prostego trójkąta prostokątnego o przyprostokątnych 5 i 1 kojot: Przez wierzchołek kąta prostego trójkąta prostokątnego o przyprostokątnych 5 i 12 poprowadzono prostą która dzieli ten trójkąt na dwa trójkąty o równych obwodach. Znajdz stosunek promieni okręgów wpisanych w otrzymane z podziału trójkąty. Zacząłem robic tak 5²+12²=c² ⇒ c=13 potem z zaleznosci na obwody wyliczyłem x 12+z+x=5+z+13−z ⇒ 2z=6 ⇒ z=3 nastepnie z pola trojkata przeksztalcilem ze wzgledu na r

	r(a+b+c)		2P
P=		⇒ r=
	2		a+b+c

	r1		2P		2P
Trzeba znajsc		wiec robie tak r1=		a r2=
	r2		a+x+z		b+13−x+z

	r1		2P		2P		2P		15+z
powstaje		=		/		⇒		x
	r2		3+12+z		5+10+z		3+12+z		2P

	P1
po skroceniu wychodzi ze		a teraz wyliczam pola ale najpierw potrzeba mi wysokosci
	P2

wiec licze je z podobienstwa trojkatów

H1		5		15
	=		⇒
3		13		13

H2		12
	=		i liczac to dalej i potem majac wysokosci pole nie wychodzi takie jakie
10		13

	10
powinno wiec i stosunek tez a powinien byc		.
	3

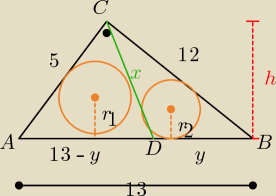Eta: x+5+13−y= x+12 +y => 2y= 6 => y=3 |AD|= 10 i |DB| =3 i 2p −−− obwód trójkątów

	PΔADC		PΔDBC
r1=		.... r2=
	p		p

r1		PΔADC
	=
r2		PΔDBC

te trójkąty mają wspólną wysokość h

	r1		10
to otrzymasz :		=
	r2		3

kojot: Rozumiem ale gdyby przyjac wysokosci inne wysokosci wtedy nie beda rozne i niechce to wyjsc

kojot: sorry wysokosci beda wlasnie rozne i niechce wyjsc