Oblicz długość odcinka CD, jeśli wiadomo
Mariusz: Na przedłużeniu przeciwprostokątnej AB trójkąta prostokątnego ABC obrano punkt D tak, że
długość odcinka BD=BC. Oblicz długość odcinka CD, jeśli wiadomo, że długość odcinka BC=15 cm
oraz AC=8 cm.
9 maj 22:25
roman:
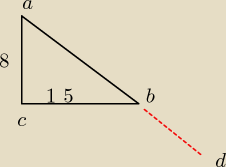
Tales ....
9 maj 22:45
roman: przynajmnie mi się tak wydaje ,..... ale wiesz pewności nigdy nie ma

9 maj 22:45
roman: IBDI=15 zapomniałem jeszcze dodac na rys
9 maj 22:48
roman: nie przecierz pitagorasem tez to zrobic mozna
9 maj 22:49
roman: pitagorasem obliczysz IABI =17
9 maj 22:53
ICSP: mi wychodzi U{120}√17}{17}
9 maj 22:58
9 maj 22:58
roman: czy te przedłużenie musi być koniecznie tak a nie mogłoby być w pionie >?
9 maj 23:00
roman: ale wątpie .///
9 maj 23:01
roman: a możesz mi powiedziec skąd masz √17 >?
9 maj 23:02
roman: podbijam
9 maj 23:05
roman: a sobie podbije jeszcze raz ...
9 maj 23:05
ICSP: z twierdzenia talesa.
9 maj 23:06
roman: szczerze mówiąc to nie łapie

9 maj 23:17
ICSP: ja czekam aż ktoś lepszy mój wynik potwierdzii.
9 maj 23:18
roman: a są lepsi .... ok jutro ja też sprawdzę

9 maj 23:19
ICSP: zaraz może Godzia złapię

Niech tylko powie czy dobry wynik.
9 maj 23:19
Godzio:
Może lepszy nie jestem, ale wynik dobry

9 maj 23:21
ICSP: jupi


Jednak jeszcze coś tam umiem obliczyć

9 maj 23:22
roman: ale może mi ktoś powie jakie stosunki boków tu zaszły >?
9 maj 23:22
roman: dzięki ....
9 maj 23:24
Godzio:
Ja tam zrobiłem to z cosinusów, bo Talesa to średnio tu widzę
9 maj 23:25
ICSP:
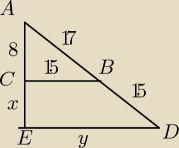
(8+x)
2 + y
2 = 1024
| | 120 | |
po wyliczeniu : x = |
| |
| | 17 | |
| | 120√17 | |
twierdzenie Pitagorasa i wychodzi |
| |
| | 17 | |
9 maj 23:26
Godzio:
A chyba że tak

9 maj 23:26
ICSP: z twierdzenia cosinusów to będzie tak:
cos180 − α = −cosα
x oznaczamy CD
| | 15 | |
x2 = 152 + 152 − 2 * 15 * 15 * (− |
| ) ? |
| | 17 | |
9 maj 23:30
roman: bardzo dziękuję
9 maj 23:30
Anna:
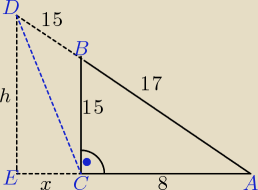
| AB | | AD | | 17 | | 17+15 | |
| = |
| , czyli |
| = |
| |
| BC | | DE | | 15 | | h | |
17h = 32*15
CD
2= h
2 + x
2
| | 480 | | 120 | |
CD2 = ( |
| )2 + ( |
| )2 |
| | 17 | | 17 | |
9 maj 23:30
ICSP: Witam Anne


9 maj 23:31
Bogdan:
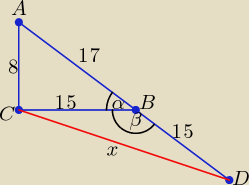
β = 180
o − α
Trzeba tu wyznaczyć dlugość odcinka CD.
9 maj 23:32
Anna: Witam, po dłuższej nieobecności.

9 maj 23:34
Bogdan:
Witaj
Anno z
ABBA 
9 maj 23:36
Eta:
 Anno
Anno
9 maj 23:37
Anna: Oooo !
! Pozdrawiam Was bardzo serdecznie,
Eto i
Bogdanie 

9 maj 23:43
Godzio:
Przyłączam się do powitania

9 maj 23:44
Anna: Witam Cię również
Godzio i gratuluję pięknie zdanej matury

!

Nie mogło być inaczej!

9 maj 23:49
Godzio:
Dzięki

W sumie mogło być lepiej

9 maj 23:49
głupi :
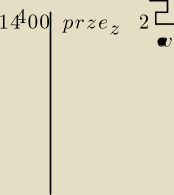
| | 244800 | |
przepraszam za swoje głupie pytanie ale ja nie wiem jak z |
| = wyszło |
| | 289 | |
no rozmumiem ze pierwsze co zrobiliscie to dzielenie przez 17 no i jest
| 14400 | |
| no a dalej jak może tak ale ja się już pogubiłem
|
| 17 | |
9 maj 23:51
głupi : sorry za ostatnie zdanie chodzi ze nie wiem jak skracaliście do waszej ostatecznej postaci
9 maj 23:53
głupi : poszli już wszyscy spac

9 maj 23:54
Anna: Ponieważ: √244800 = √100*16*9*17 10*4*3*√17 = 120√17
9 maj 23:56
głupi : a... w ten sposób .... dziękuję
9 maj 23:57
głupi : a jest jakaś zasada na tego typu obliczenia
9 maj 23:58
głupi : jakby co będę jutro ... to spr...
10 maj 00:01
Anna: Można różnie kombinować z tak dużą liczbą, np. dla ułatwienia można rozłożyć ją na czynniki
pierwsze (jak to zacząłeś wyżej). Tak, czy inaczej, trzeba rozłożyć na mniejsze czynniki,
które pozwolą się pierwiastkować.
10 maj 00:03
głupi : mhm
10 maj 08:41
 Tales ....
Tales ....



 Niech tylko powie czy dobry wynik.
Niech tylko powie czy dobry wynik.


 Jednak jeszcze coś tam umiem obliczyć
Jednak jeszcze coś tam umiem obliczyć
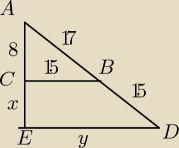




 β = 180o − α
Trzeba tu wyznaczyć dlugość odcinka CD.
β = 180o − α
Trzeba tu wyznaczyć dlugość odcinka CD.


 Anno
Anno
 ! Pozdrawiam Was bardzo serdecznie, Eto i Bogdanie
! Pozdrawiam Was bardzo serdecznie, Eto i Bogdanie 


 !
!  Nie mogło być inaczej!
Nie mogło być inaczej!

 W sumie mogło być lepiej
W sumie mogło być lepiej 

