w urnie są kule białe i czarne. Czarnych kul jest dwa razy więcej niż białych.
Wisiek: w urnie są kule białe i czarne. Czarnych kul jest dwa razy więcej niż białych. Wyjmujemy z urny
dwie kule. Jaka jest najmniejsza liczba kul w urnie, dla której prawdopodobieństwo wylosowania
| | 2 | |
dwóch kul czarnych jest większe od |
| |
| | 5 | |
9 maj 20:25
Eta:
najmniej musi być 9 kul: 3 białe i 6 czarnych
9 maj 21:34
Wisiek:
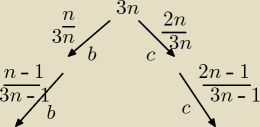
Kurczę ale jak to wyliczyłeś bo ja próbowałem drzewkiem:
N = białe
2N = czarne
czyli:
| n | | n−1 | | 2n | | 2n−1 | | 2 | |
| * |
| + |
| * |
| > |
|
|
| 3n | | 3n−1 | | 3n | | 3n−1 | | 5 | |
| n2−n | | 4n2−2n | | 2 | |
| + |
| > |
|
|
| 9n2−3n | | 9n2−3n | | 5 | |
| 5n2−3n | | 2 | |
| > |
| / * 5
|
| 9n2−3n | | 5 | |
| 25n2−15n | |
| >2 / * (9n2−3n)
|
| 9n2−3n | |
25n
2−15n>18n
2−6n
7n
2−9n>0
n(7n−9)>0
| | −n2−n | |
Czyli coś jest nie tak... dodam że gdyby było |
| to wtedy by sie wszystko |
| | 9n2−3n | |
zgadzało tylko że nie pasuje mi to z drzewkiem. Mógłbyś Eta albo ktokolwiek inny wyjaśnić mi
mój błąd ?
9 maj 22:33
10 maj 00:02
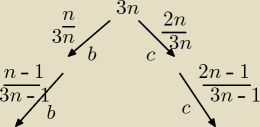 Kurczę ale jak to wyliczyłeś bo ja próbowałem drzewkiem:
N = białe
2N = czarne
czyli:
Kurczę ale jak to wyliczyłeś bo ja próbowałem drzewkiem:
N = białe
2N = czarne
czyli: