/ zaq: przekątne podstawy i krawędzie boczne ostrosłupa prawidłowego czworokątnego są równe.Wiedząc że wysokość tego ostrosłupa ma 3√6cm długości wyznacz: a)dł.krawędzi bocznej ostrosłupa b)dł.krawędzi podstawy c)cosinus kąta jaki tworzy ściana boczna z podstawą

Nie jestem mądry: a) 6√2 b) 6 c) √7

zaq: a czy mógłbyś mi to rozpisać ,bo męczę sie nad tym i nie mogę dojść końca:(:(Proszę!

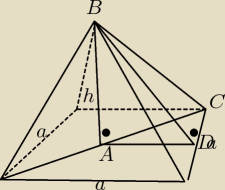
Nie jestem mądry: Krawędz podstawy oznaczamy jako a. Z zadania wiemy że w podstawie mamy kwadrat o długości boku a więc jego przekątna ma długość a√2 i jest równa krawędzi bocznej h=3√6

	a√2
Bierzemy trójkąt ABC BC= a√2 AC=		( wysokość w ostrosłupie czworokątnym
	2

prawidłowym dzieli przekątną podstawy na dwie równe części)

	a√2		2a2		3a2
h2=(a√2)2− 9		)2= 2a2−		=
	2		4		2

	3a2
54=
	2

108= 3a² a²=36 ⇒ a =6 ( mamy obliczony podpunkt b oraz a ) Teraz trójkąt BDC BD²=(6√2)²− 3²= 72−9=63 ⇒ BD= √63 cosinus kąta sciany bocznej z podstawą jest stosunek AD do BD

	1
AD=		a=3
	2

	3		3√63		√63
cosα=		=		=
	√63		63		21

Chyba nie zrobiłem błędów obliczeniowych

zaq: ok wielkie dzięki za pomoc

roman: może mi ktoś powiedzieć skąd tam się wzieła 9−tka >?

Nie jestem mądry: prze przypadek się kliknęło powinien być nawias (

roman: a ja już myślałem ze zle policzyłem .... ok dzięki

roman: łe sorry że jeszcze raz komuś zawrócę głowe ale nie wiem co się stało z tym minusem miedzy 2a²

	2a2
a
	4

roman: podbijam

Nie jestem mądry:

	2a2
2a2−		o to chodzi ?
	4

roman: tak tak

Nie jestem mądry: zwyczajnie wykonujesz odejmowanie...

	2a2		a2
przy czym		=		bo 2 i 4 się skrócą
	4		2

4a2		a2		3a2
	−		=
4		4		4

Nie jestem mądry: zamiast 4 dwujka ma być

roman: dziękuję

roman: Nie jestem mądry ⇒ dwójki