Rownanie prostej równoległęj do osi OX
bleeeeee: Napisz równie prostej równoległej do osi OX i przechodzącej przez punkt K(2,1)
8 maj 22:07
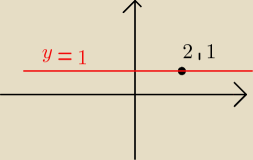
bump: y=2
8 maj 22:12
bump: sorry y=1
8 maj 22:12
romanooo: | | 1 | |
 y= |
| x chyba... |
| | 2 | |
8 maj 22:14
romanooo: znaczy, na pewno haha
8 maj 22:15
bump: wtedy nie bedzie rownolegla do osi OX
8 maj 22:15
romanooo: aaa
równoległej

to jest dobrze

myślałem że przechodzącej przez (0,0)

8 maj 22:15
bleeeeee: drodzy pomocnicy! nadal nie wiem jak poprawnie rozwiązać to zadanie

8 maj 22:20
Kejt: współczynnik 'a' musi być równy zero.
f(x)=1
8 maj 22:20
bleeeeee: aaa

8 maj 22:21
bump:

8 maj 22:23
bleeeeee: A w przypadku gdy chcemy napisac równienie prostej równoległej do osi OY, wspolyczynnik
kierunkowy ulega zmianie?
8 maj 22:26
bump: wtedy zamiast y bedzie x np x=2
8 maj 22:26
bump: a wspolczynnik oczywiscie 0
8 maj 22:27
Paweł: Nie ma takiej prostej, nie spełnia warunków. Dla każdego argumentu przyporządkowana jest jedna
wartość, gdyby prosta była równoległa do osi OY, wtedy dla jednego argumentu było by
przyporządkowane nieskończenie wiele wartości.
8 maj 22:30
bump: ale jest taka prosta po prostu nie ma takiej funkcji
8 maj 22:31
Grześ: Wtedy nazywa się to "równaniem prostej", a nie funkcją

8 maj 22:32
Eta:

8 maj 22:32
bump: Eta chyba potwierdza

8 maj 22:34
 y=
y= to jest dobrze
to jest dobrze  myślałem że przechodzącej przez (0,0)
myślałem że przechodzącej przez (0,0) 






